
陳方正(2009)繼承與叛逆──現代科學為何出現於西方?北京市:三聯書店。 ISBN 978-7-108-03047-4

這本書是陳宜良老師推薦的,卻是由李志豪教授轉告的。 他從 twSIAM 的一個 chat room 複製了陳老師的貼文:
這本書和序都值得拜讀。我對徐光啓很感興趣,他是中國體認到理學中格致本質是數學的人。他的幾何原本序值得放在高中國文教材中。單維彰近作:數學中的文化脈絡也有利瑪竇、徐光啓相關的研究,值得一讀。另外,近代中國大格局的數學家與科學家只孕育在 1930-40 年代,這也是一個有意思的課題。台灣為何不能?以色列為何行?這些文化因素值得深入分析。 (2020/05/19)
那段時間,我正為徐式寬教授召開的「教育的古典與現代」座談會(2020/05/30)準備文稿, 這本書以及余英時先生的序言,正好提供了破題的動機。 以下,我便以那天的報告全文充當這本書的讀書心得。
從歷史探究數學教育的現象
教育的古典與現代之對話座談會
單維彰.民國 109 年 5 月 30 日
筆者固然同意余英時認為「李約瑟問題」只能是一個假問題(pseudo-question)(2010:頁 153)也同意歷史方法似乎不宜用來研究「沒發生」的事情,但是在教育領域內,一旦想要探究課程規劃與教材教法所受的文化影響,似乎無法避免同樣類型的問題:為什麼中國的自然哲學與工程技術沒有「數學化」?為什麼中國的菁英階級曾經如此輕視數學?那又為什麼在如今的華人社會中,數學在學校教育裡受到如此器重?但是它的地位似乎完全建立在考試的需求上,一旦完成或失去了考試的價值,為什麼一般人對數學的態度又恢復成傳統的輕視?數學教材內容的編撰,是否一直存在傳統上學習「經學」的影子?也就是試圖將經典知識作一全面性的、系統性的盤點。探究這些問題,不僅為教育史的興趣,更是為了藉由釐清病因,設法從根本上改善數學教育的內容與方法。
如果確實如前面所說,數學在學校教育之中所受的器重,主要是功能性的、外在的。如果說「十九世紀晚期以來科學在中國的發展史,事實上便是西方科學不斷移植到中國的過程,從局部一直擴展到全方位」(余英時,2010:頁 158),此處的「全方位」似乎只能理解為領域性的,而不是就人口而言的全面性。在擴展到全方位之後的第一個世紀裡,已經出現少數成功的個案,可藉以證實從華人文化中成長的個體,仍有可能運用新習得的數理知識與技能,在新出現的外來文化中博得尊敬。然而,一個世紀之後,可否藉由教育,從領域的全方位轉向人口的全面性?從功利主義的外在誘因轉化為自我實現的內在動機?
最後再回顧一次「李約瑟問題」。向來的議論似乎都著眼於文化、歷史、乃至於宗教,想必已經有人從政治與經濟的層面來解釋此現象。這種進路已經至少有一位先行者可供參考:新經濟史;它用制度來解釋經濟發展史。誠如孟子所言「出則無敵國外患者,國恆亡」。這裡說的是東周列國,恰如歐洲各國。中國太早統一,而且人心習慣了大型帝國。大型帝國的中國雖然不能說沒有敵國,但統合之後實在質量太大,使得敵國的威脅並不嚴重也不恆常。歐洲諸國則處於持續競爭狀態,沒有一國有實力統一歐洲(法國先試了一次,然後德國試了兩次,最近德國把鉛彈換成銀彈,且讓我們看看它這次是否忠能成功),而語言文化與地理的接近又使得新知識與新技術容易傳播,因此發明者無法保持太久的優勢。歐洲在封建小國的競爭中創造了數學與科學進步的需求,中國則以一部《九章》足堪應付帝國管理的一切需求,在缺乏「敵國外患」的天地間,緩緩地亡於自己的偉大。筆者相信已經有更專業的學者,做過前述理論的研究,只是身為門外漢而不知道適當的文獻。
如果以上假設成立,則華語文化內的吾人,不但在個體基因上、腦神經結構上已經確證可在數理領域出類拔萃,整體社會人群也不無習得並內化數理思維精神的的可能。中國典籍將數與算的概念上推到伏羲和黃帝,怎會不重視算學?中國在帝國管理與民生軍事的技術上,曾經維持了很長時間的全球領先,怎可能沒有數學教育?如今的狀態常歸咎於明代的轉捩,筆者認為這是客觀事實,但認為應關注的是制度層面的影響;對於科舉和太學制度的批判,已經算是普遍了(武錫懷、郭宗明,2003:頁 121),但筆者仿新經濟史的觀點,猜想政治與經濟制度具有更高的解釋力。整個社會人心的轉變,需經由教育,但不能僅限於學校,而要使教育如慮篩般逐年轉化人心,逐漸轉化人群對數學與科學(自然領域的、社會領域的)的態度改變,最後促成更適當的制度。
* * *
筆者認為在徐光啟的時代,《幾何原本》就是《基礎數學》的意思(單維彰,2020:頁 173)。在中文的脈絡裡,數學曾是算術的意思,而算學是數學的名稱。因為徐、利選取的譯名,加上日本正式賦予「幾何」形學的意涵,清末之後,幾何的意義就從「有多少」流變為「形學」了,它正式成為 Geometria 的音譯。至於代數、微分、積分都出自晚清李善蘭(1810—82)之手而沿用至今。「數學」和「科學」都是從日本引進的名詞,但是它們與「算學」和「格致」併用了至少三十年,歷經一整代人。例如王國維在 1901–2 年之間翻譯日本人藤澤利喜太郎的《算術條目及教授法》(原著出版於 1895 年,Wikipedia-JA)採用了日文直譯至中文的「算術」而非中算傳統下的「數學」。就史料而言,王國維的這份譯作是第一部中文的數學教育專書(代欽、松宮哲夫,2017:頁 206),但是它有多大的影響力?譬如說,它促使「算術」取代「數學」的意義了嗎?「數學」正式取代「算學」而被定為這一門學術領域的名稱,從 1933 年 4 月開始進入機構內的討論,一直到 1935 年 9 月該公布結論的時候,還在掙扎而沒有定論,故在公布的官方標準詞彙表內還是兩案並存。直到 1938 年 9 月,抗日戰爭中遷到後方的教育部重啟調查,才在 1939 年 6 月以「多數決」採用了「數學」,並通令全國相關單位照辦。但詳視該次調查的書面記錄,因為在戰亂中,故採通訊投票,收到的 28 票中,「數學」14 票、「算學」13 票(任南衡、張友余,1995:頁 34)。前輩們對此領域名稱的糾結,由此可見一斑。而學術問題之獨立於政治之外(「數學」來自日本,當時正在對日作戰),也由此可見一隅。
在明末以「格致」指稱西方的自然哲學的源頭,以及在晚清自強時期的反省,乃至於在維新之後被「科學」取代的過程,已經多有著述,似乎可以令人滿足了。可是數學與自然哲學如何被整併為「數理」?而「理學」如何從宋明的學問轉化成今日一般大學中「理學院」內的學科,則還不太清楚。「科學」很清楚從日文而來,但是「數理」卻已經出現在李善蘭翻譯牛頓《自然哲學中的數學原理》的書名上:《奈端數理》;難道這兩個字就是「數學原理」的縮寫嗎?自從徐光啟與利瑪竇將相等的比稱為「同理」之比,「理」這個字就跟數學發生了許多糾結。但徐、利的用字也許並無深意,只是口語「同理」的延伸而已:例如說「兩顆糖賣 3 元,同理四顆糖賣 6 元。」這個字是否導致了後來的有理數、無理數之名稱?還不是十分確定。這三個「理」─宋儒「理」學,「理」學院,有「理」數─看來各有脈絡,彼此無關。是這樣嗎?
前面說過數學各分支的知識及中文譯名都在晚清到齊了,其實包括機率在內。第一部中文的機率知識來自華蘅芳在 1880 年協助翻譯的《決疑數學》,當時將「機率」翻譯為「決疑數」,這個譯詞沒有傳下來。這部書內含機率發展史,簡述了包括棣美弗、拉普拉斯、貝斯在內的貢獻,並且已經涉及連續型機率分布函數(正規分布函數及它的積分表);此書的一份重要應用範例是保險學。相對於其他數學書籍,這一部書似乎相對地沒沒無聞。當時中國可能還沒有保險業,而且機率跟槍砲彈藥似乎沒有直接關聯,所以它若是因此不受重視,也是情有可原的。晚清的數學課程,不論官方學堂還是私辦書院,目前都沒看到機率的影子。如今的機率課程是否曾經受到《決疑數學》的影響?還是後來重新引進?目前不得而知。藤澤利喜太郎的著名工作之一是是將保險學引進日本,他的《生命保險論》出版於 1889 年,這部書受過《決疑數學》影響的機會很小,因為《決疑數學》雖然在 1880 年於江南製造局完成翻譯,但是直到 1896 年「甲午戰敗」之後才印刷出版。
* * *
余英時認為中國的現代自然科學是全盤西化的結果,並無中國傳統知識對接或轉銜的歷史研究問題,這或許是正確的意見;但是數學並非如此。元朝前後傳入中原的西方數學,並沒有在文化脈絡中產生影響,而西算的傳播是從利瑪竇入華作為起點,這些意見似乎已成共識。從那時起,一直到 1845 年(道光廿五年)上海始闢租界,可以視為西算傳入中國的第壹期。在此時期,中國的博儒與疇人除了譯介西算新知以外,幾乎都曾努力將之「本土化」;翻譯工作本身也經常內含本土化的意圖。許多才智之士為論述「西學中源」而皓首窮經,以後見之明來看,甚為可惜。但是,這些前輩的工作,很可能具備教育價值:依循著華人的文化脈絡和語言習性來學習西方數學,或有可能降低門檻或減緩坡度。是否有人以前述觀點重新開採過第零期的數學文獻?經由上海租界,西算第二度大量傳入中國。關鍵性的微積分、解析幾何與代數、機率與統計,此時才傳入中國。此時有幸直接與洋人合作從事第一手西算翻譯工作,而且又難得具備深厚中算功底的人士,可能首推李善蘭,其次華蘅芳。除了極少數的幾位幸運才士之外,這段時期的才智之士都靠自學,而自學的「西書」主要就是前述那幾位協助翻譯的中文書籍;到了後期,能讀東文(日文)的人才稍多,得以從日文學習,或者將知識從日文譯介進來,但筆者認為自學仍屬主要學習方式。我還不知道該將此西算傳入的第貳期劃在哪裡結束?選擇之一是 1917 年:首位獲得數學博士學位(哈佛大學)的胡明復歸國。
制度化的數學教育是由上而下展開的,這也標示著自強運動(洋務運動)的開始。以學習外語為教育目標的京師(北京)同文館、上海廣方言館、廣東同文館先後成立於同治元年(1862)、二年、三年,但是後兩所學校從一開館就規定了算學課程(以西算為主),天子腳下的京師同文館則在歷經激烈的辯論攻防之後,才在同治六年(1867)在館內增設了天文算學館,延聘李善蘭擔任教習(唯一的一名教授席位),次年到任。
當時絕大多數的書院已經實際上成為科舉考試的補習班,我們要避免對書院的教育功能產生太多幻想。因為科舉沒有算科,因此不能指望書院主動在課程中增加算學。書院內的算學教育在光緒朝(1875年之後)才開始出現(李兆華,2005),而且主要集中在甲午年(1894)之後,所以書院在數學教育所發揮的影響力,可能暫時不必深究。
即使是官辦的算學學習機構,也要小心別賦予過度期待。同文館的招生相當困難,原因之一是菁英階級的主流意識仍認為「從夷人學」是不體面的,但更根本的原因是它不等於「功名」,即使畢業後可獲分發官職,也因為不是出身「正途」而低人一等。例如同文館的首屆畢業生張德彝(1847—1918)曾擔任光緒帝的英文教師,最後官至二品,擔任英國大使(1902—06),但晚年仍告誡子孫「國家以讀書能文為正途,...余愧與正途為伍,而正途亦間藐與為伍。人之子孫,或聰明,或愚魯,必以讀書為要務」(樊洪業,2000:頁 13)。這樣的「讀書為考試,考試為升官發財」的人生規劃,在中華文化裡根深蒂固,絕不會因為改個國號就幡然一新。例如蔡元培於 1916 年擔任北京大學校長時,特別「此地無銀三百兩」地宣告:「大學教育不是舊時科舉考試的替代品,並不是升官發財的捷徑」(徐中約,2002:頁500)。此一情緒是否換種形式延續至今?
* * *
早期的西算學堂,唯有李善蘭坐鎮的京師同文館能提供微積分等級的課程。上海和廣州都會薦送優秀畢業生到京師的天文算學館去深造,例如李善蘭的主要傳人席淦便是從上海送來的學生,於同治七年到館。包括李善蘭在內的第一代西算學者,主要承繼了中算的傳統,於西算則出於傳教士的口授加上自己的領悟,而口授者本人可能也是自學成材的。考量這些因素,對於最早的數學教材教法,也不宜懷抱太多的憧憬。大體而言,當時的教材顯得太深太純:以知識的全面總整為要,雖然言必稱「西人制器…皆從算學出」但最後可能淪為人云亦云的信仰,不見得知道如何實際應用數學。及至甲午戰敗,自強運動被判為徹底失敗,社會上更積極想要維新的情緒,只能使得數學教材更加艱深。根據《同文館算學課藝》,天文算學館的教材包括從中算「句股容圓」衍生出來的「勾股十三率」,如下圖(李兆華,2005:頁 47),從直角三角形 ABC 及其內切圓、該圓的外切正方形,可辨識大大小小的 13 個直角三角形,每個三角形各有 13 個可問的邊長(包括其內切圓直徑),如此產生 條公式。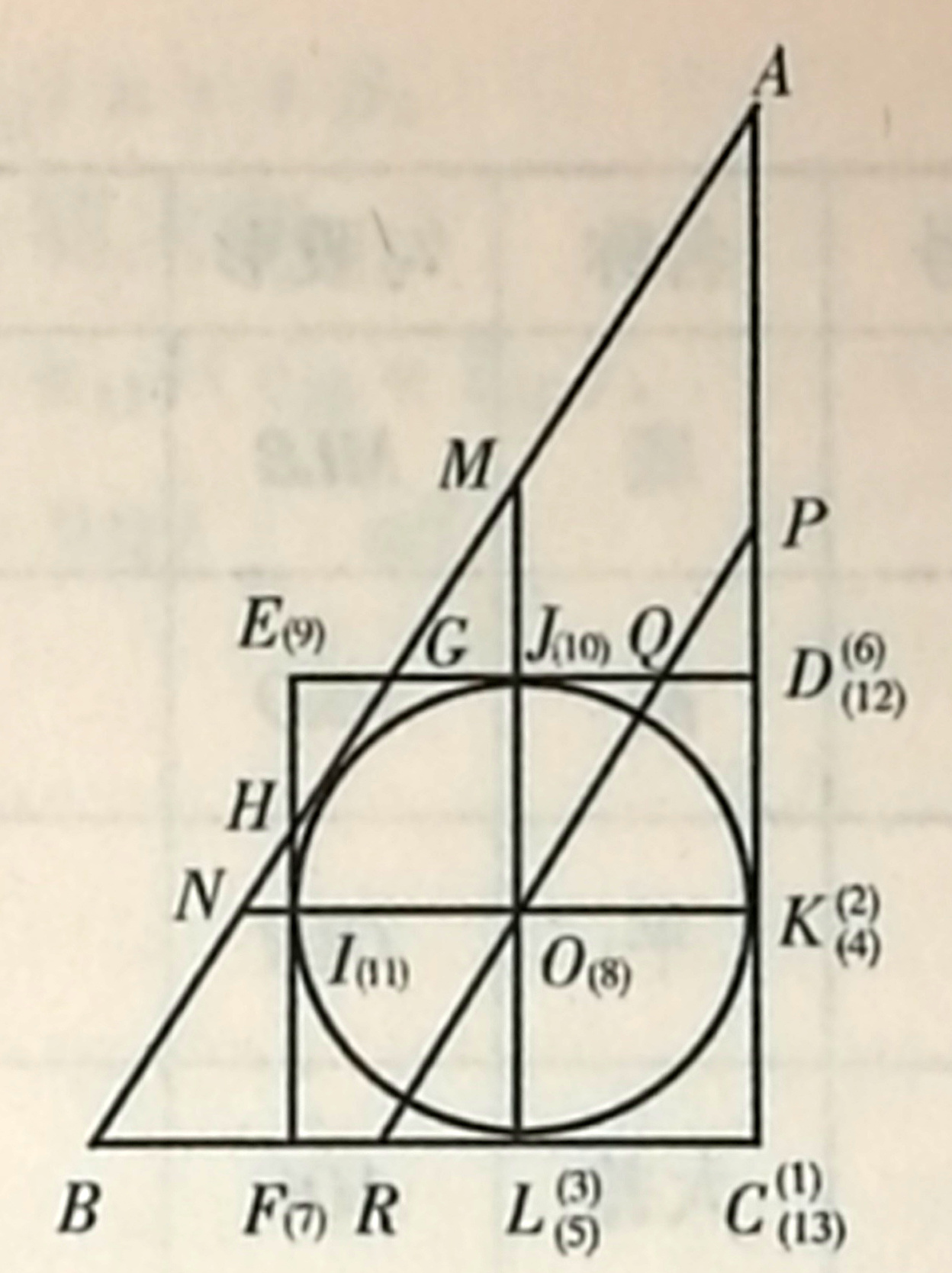
「勾股十三率」可能並非共同必修教材,可是《課藝》的教材特徵由此可見一斑,而直到今天臺灣的數學教材仍然依稀可見此特徵。同時期的歐洲數學教材,也有這種「全面性知識總整」的風格嗎?當時日本的影響還沒進來,同時期的日本也正從和算轉為西算,其教材可有類似的風格?筆者猜想這是中國數學教材的自發性特徵之一,而且它流傳至今。
筆者曾猜測高中數學課程中的「綜合除法」來自於李善蘭對於中算的整理,而且可能也只有他能看得出來此中算算法與微分概念的關係。如今,從《課藝》中可得天文算學館之教材包括綜合除法的證據,當時似乎稱為「正負開方術」(李兆華,2005:頁 57),尚不確定是否當年即以此算法連結多項式函數的微分公式?如果是,則此處或許是中算與西算的一個重要銜接點,而這個節點幸運地沿著中學數學課程傳遞至今。
* * *
臺灣的數學教育,至少在於中學階段,受日本統治時期的影響,並不如想像中的大。光復以後,中學教育大體上完全由國民政府的教育體系取代。因此臺灣的數學教育可以放在中國的數學教育脈絡中研究。中國的數學教育,就像所有的中國近代社會、經濟與文化發展一樣,全都在 1935 年前後顯得朝氣蓬勃而情勢看好(僅就城市而言)。可是所有的發展都因為抗日戰爭嘎然而止。戰後則立即陷入國共內戰,雙方喘息甫定之後,中國先後陷入十年文革與急起直追的運動,臺灣則先後汲汲於經濟成就與政治議題,雙方似乎都是匆匆忙忙跌跌撞撞地闖進了廿一世紀,於是都沒有機會以充裕的時間和自由度,靜下心來重新思考 1935 年代中斷的教育議題,甚至重新檢視 1905 年代關於教育的辯論。筆者希望從大環境的視野中,以歷史方法探究數學教育的現況,並試圖提出改善的議案。
參考文獻
- 代欽、松宮哲夫(2017)數學教育史─文化視野下的中國數學教育。北京市:北京師範大學出版社。
- 任南衡、張友余(1995)中國數學會史料。南京市:江蘇教育出版社。
- 余英時(2010)環繞著「李約瑟問題」的反思──陳方正《繼承與叛逆》序。收錄於《中國文化史通釋。Hong Kong: Oxford Univ Press。
- 李兆華(2005)中國近代數學教育史稿。濟南市:山東教育出版社。
- 武錫懷、郭宗明(2003)數學史與數學教育。成都市:電子科技大學出版社。
- 徐中約(2002)中國近代史(下冊)。香港:香港中文大學。
- 單維彰(2020)文化脈絡中的數學。桃園市:中央大學出版中心。
- 樊洪業(2000)科學舊蹤。南昌市:江西教育出版社。
- Wikipedia-JA (2020). 藤沢利喜太郎。造訪於2020年5月23日:https://ja.wikipedia.org/wiki/藤沢利喜太郎
陳教授學富五車,讓我好生崇敬。他的見識方向與探究進路,都跟我同路,當然他在前方。陳教授七十歲出版這部巨著,我也想要寫一部這樣的書;以陳為師,我還可以再努力十二年。這部書輕手消解了「李約瑟問題」並且開啟了自己的議題,也就是此書的副標題。
這部書裡幾項觀點,已經同樣被寫在《文化脈絡中的數學》裡。例如
《繼叛》西方與中國科學的真正分水嶺不在近代,而遠在公元前四五世紀之間甚或更早,譬如說孔子和畢達哥拉斯在世的「軸心時代」。(頁 XXII)《文脈》畢氏與印度的悉達多(釋迦牟尼) 和中國的孔丘(孔子)幾乎是同代人,他們幾乎在同一時期開創了三支文化傳統。 ... 所謂畢氏「學派」也可以視為一個「教派」,畢達哥拉斯簡直是創立了一個崇拜「數」的宗教。
《繼叛》西方科學傳統最特殊而迥然有異於中國...[的]可能方向則是宗教。畢達哥拉斯視宇宙奧妙之探索為超脫輪迴,獲得永生之道,其教派視數學發現為絕頂秘密...對於學園內外的教派傳人而言,數學與天文奧秘、規則是如何值得凝神竭智,畢生全力以赴的頭等大事也就不言而喻了。(頁633)
《文脈》畢達哥拉斯的思想雖然沒有以宗教的形式傳遞下來,但是他就像釋迦牟尼和孔子一樣,實際上開創了一種文化。...把數學提升到屬靈的境界,不但讓數學從實用的束縛中解脫出來,更開啟了理性辯證上的需求:事關信仰的絕對與心靈的純粹,豈能容許一絲懷疑?於是,希臘人開創了數學「證明」的形式,也賦予「證明」至高的價值。(頁106)
我在陳教授的書裡一再映證我的思路有前人的背影,心下踏實許多。但是,即使有這部巨著在前,我仍然認為還有未竟之言,等著被寫出來。
難得中央大學有人跟我競爭這本書,導致我不能續借,只好快快讀完。