這個月我要跳回去講複數(原訂的三角函數順延)。 因為打鐵要趁熱,我想回應五月號『文化裡遇見數學』關於三次方程式的公式解 (pp.354--8)。當初介紹虛數的時候 (本欄四月), 就想要提起這段故事,並且闡述高斯 (Carl Gauss) 的一個見解: 虛數 (imaginary number,直譯為「想像的數」) 並不全然是人類的想像, 它是實在地存在的。他舉的例子,就是三次方程式的公式解: 當公式的中間步驟產生實數的時候,方程式其實有一對複數根; 當公式的中間步驟產生虛數的時候,方程式其實有三個實數根。 如果你想要走進三個實數根的殿堂,就必須穿越虛數的門廊。 透過三次方程式,實數和虛數互相映照的關係,被明確地表現出來。 所以虛數和實數一樣是數學內在結構裡的本質元素, 而不是人類想像出來的怪物!
我當時認為這個故事,偏離我預定的目標太遠 (數學中最美的等式),所以割捨了。
欣然見到英家銘和蘇意雯兩位老師,恰好為我補足了所有需要的基礎,
真是天作之合啊 (我們真的不是約好的)。
歷史故事和公式解的推導,都被英、蘇兩位老師 (不是兩國) 講完了,
我們就從 357 頁開始。只考慮
![]() 這種形式的 (實係數) 三次方程式,以後就稱它為 (P),
其中 p 是正數,q 不管是正還是負還是零都可以;
我們馬上就說明古人要求 q 是正數的原因。令
這種形式的 (實係數) 三次方程式,以後就稱它為 (P),
其中 p 是正數,q 不管是正還是負還是零都可以;
我們馬上就說明古人要求 q 是正數的原因。令
且
稍後我會舉一個實際計算的例子。請先忍耐著看完符號上的推理過程。
把 (P)「改裝」成函數的形式
![]() ,
則 y=f(x) 的函數圖形與 x 軸的交點就是 (P) 的根,
此後我們就稱這條曲線為 C。
運用一點點微分學,我們會知道,當 p 是正數,
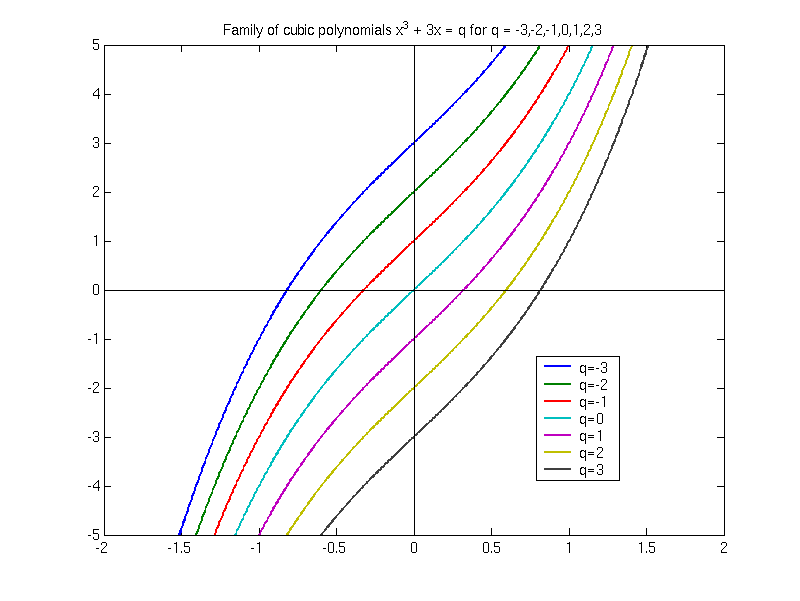
C 永遠漸增,因此只會跟 x 軸產生一個交點;(P) 只有一個根。
因為 C 的 y 截距 (代入 x=0) 就是
,
則 y=f(x) 的函數圖形與 x 軸的交點就是 (P) 的根,
此後我們就稱這條曲線為 C。
運用一點點微分學,我們會知道,當 p 是正數,
C 永遠漸增,因此只會跟 x 軸產生一個交點;(P) 只有一個根。
因為 C 的 y 截距 (代入 x=0) 就是
![]() ,
所以若 q 為正數,交點必在 y 軸的右邊,也就是有正根;
若 q 為負數,交點必在 y 軸的左邊,也就是有負根。
一圖解千言,讓我們看一張圖吧(如下)。
我以 p=3 為例,為讀者畫了 q=3,2,...,-3 七種情況的曲線,
也就是七種 C。
觀察 q 是負數的時候有負根,q 是正數的時候有正根。
然而,現在我更想要強調的是:這些方程式都只有一個根。
,
所以若 q 為正數,交點必在 y 軸的右邊,也就是有正根;
若 q 為負數,交點必在 y 軸的左邊,也就是有負根。
一圖解千言,讓我們看一張圖吧(如下)。
我以 p=3 為例,為讀者畫了 q=3,2,...,-3 七種情況的曲線,
也就是七種 C。
觀察 q 是負數的時候有負根,q 是正數的時候有正根。
然而,現在我更想要強調的是:這些方程式都只有一個根。
同樣也是運用一點點微分學,我們會知道,當 p 是負數,
C 就會往下折和往上折:
在 C 往下折的轉彎處,有一個山峰;在它往上折的轉彎處,有一個山谷;
在山峰的左邊,C 無盡下降,在山谷右邊,C 無盡上升。
請看前述網頁的第二幅圖。
學過一個月微積分的讀者,都能算出來,山峰一定發生在 y 軸左邊的
![]() 處,而山谷一定發生在對稱的 y 軸右邊
處,而山谷一定發生在對稱的 y 軸右邊
![]() 處。想像著坐標平面上的曲線 C,如果它的山峰發生在 x 軸下方,
則山谷更低也在 x 軸下方,
所以 C 和 x 軸只能有一個交點,而且一定在
處。想像著坐標平面上的曲線 C,如果它的山峰發生在 x 軸下方,
則山谷更低也在 x 軸下方,
所以 C 和 x 軸只能有一個交點,而且一定在
![]() 的右邊;所以 (P) 只有一個正根。
如果它的山谷發生在 x 軸上方,山峰更高也在 x 軸上方,
所以 C 和 x 軸只能有一個交點,而且一定在
的右邊;所以 (P) 只有一個正根。
如果它的山谷發生在 x 軸上方,山峰更高也在 x 軸上方,
所以 C 和 x 軸只能有一個交點,而且一定在
![]() 的左邊;所以 (P) 只有一個負根。
的左邊;所以 (P) 只有一個負根。
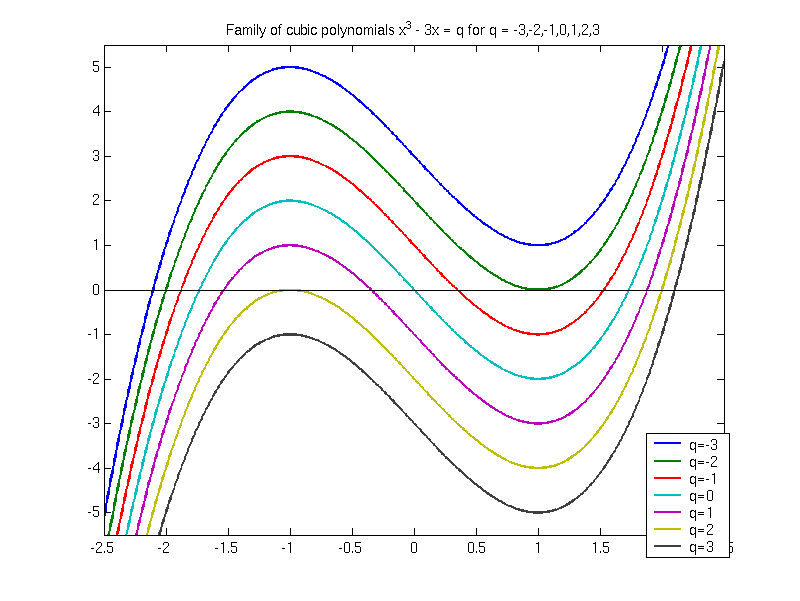
有趣的是,如果山峰高過了 x 軸,但是山谷卻低於 x 軸,
則 C 就會和 x 軸有三個交點:(P) 就會有三個根!
只要求解兩個不等式
![]() 和
和
![]() 就會發現,原來這種有三個根的情況,就是
就會發現,原來這種有三個根的情況,就是
![]() 的情況!所以
的情況!所以
![]() 其實可以當作 (P) 有幾個根的「判別式」!
若
其實可以當作 (P) 有幾個根的「判別式」!
若
![]() 則 (P) 只有一個根,若
則 (P) 只有一個根,若
![]() 則 (P) 有三個根。我留給有興趣的讀者自己去推論
則 (P) 有三個根。我留給有興趣的讀者自己去推論
![]() 的情況。
的情況。
高斯的話就是指這裡:當 (P) 有三個根, u 和 v 的計算卻面臨負數的平方根,也就是虛數! 但是具有虛數的 u 和 v 最後卻能幫我們找到 (P) 的三個根。 如果 u 和 v 的計算正常地得到實數,(P) 反而只有一個根, 但是實數的 u 和 v 卻可以幫我們找到 (P) 的一對共軛複數根! 多麼美麗而必然的對稱關係?
舉個有數字的例子。令 p = -3,q = 1,也就是求解
![]() 。
此時
。
此時
所以
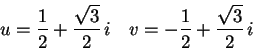
上面那兩個數很面熟嗎?它們是 60 度角的餘弦和正弦值:
記得棣美弗定律嗎?他說
高中時代只討論了正整數的指數 n, 其實 n 也可以是分數。它跟「數學中最美的等式」只有一丘之隔了, 我們還會另外講它。現在您只要驗證 n=1/2 的情況, 就請您相信 n 是任意分數都行吧:因為
根據倍角公式,等式的右邊就是
現在我們應用 n=1/3 的棣美弗定律來計算
這就是
我希望上面的例子順便表現出一種學習廣義角的動機與需求。
下個月我們回到三角函數,解釋像
![]() 這種數值是怎麼算出來的?
這種數值是怎麼算出來的?