評量5.36
- 0.4772 + 0.4987 = 0.9759
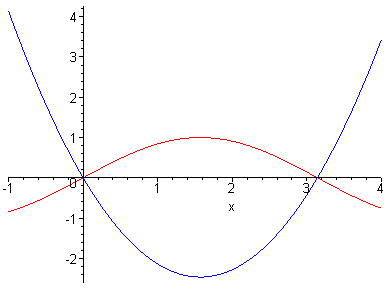
RED :sinx
BLUE:x(x-π)
評量5.37
註:因為積分步驟因人而異,所以答案不是唯一,故此答案作為參考用。
將所算出之答案微分後,等於原積分之函數即可。
- ∫(lnx/x)dx = ∫(lnx)d(lnx) = (1/2)(ln|x|)2 + c
- ∫(esinxcosx)dx = ∫(esinx)d(sinx) = esinx + c
- ∫(cos2xsin5x)dx = -∫(cos2xsin4x)d(cosx) =
-∫[cos2x(1-cos2x)2]d(cosx) = ∫[-cos2x + 2cos4x - cos6x]d(cosx) =
-(1/3)cos3x + (2/5)cos5x - (1/7)cos7x + c
- ∫[(x+7)(3-2x)(1/3)]dx = (-1/2)∫[y(1/3)(17/2 - (1/2)y)]dy (令y = 3-2x)=
(3/28)(3-2x)(7/3) - (51/16)(3-2x)(4/3) + c
- ∫[3x/(x2 - 2x - 8)]dx + ∫(3/2)d(ln|x2 - 2x - 8| + ∫[3/(x+2)(x-4)]dx =
∫[3x/(x2 - 2x - 8)]dx + ∫[(-1/2)/(x+2)]dx + ∫[(1/2)/(x-4)]dx =
(3/2)ln|x2 - 2x - 8| - (1/2)ln|x+2| + (1/2)ln|x-4| + c
另解:2ln|x+4| + ln|x-2| + c
- ∫[1/(x2 - 6x + 12)]dx = ∫{1/[(x-3)2 + 3]}dx =
∫[√3/(3y2 + 3)]dy (令x = 3 + √3y)= (√3/3)tan-1[(x-3)/√3] + c
- =
(令 y = lnx => x = ey)=
=
=
=
3(e2 - e)
- =
=
1
- (1/7)(57 - 37)
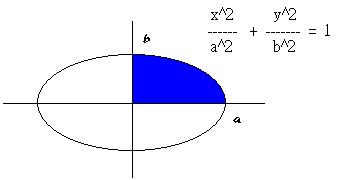
- 如圖設a,b分別為下圖中的半長軸和半短軸長,則橢圓面積 = 4 X 藍色部分面積
由橢圓一般式 : x2/a2 + y2/b2 = 1 知 :
y = b(1 - x2/a2)(1/2)
則藍色部分面積 =
(令x = asinT)=
=
所以橢圓面積 =