=epsf.tex
�DzΪ����μƾ�, �����O�N�ƾ����Φb���z�譱. ���o�]�O���y, �کԳo�Ǧ������H���ұM�`�����D. �o�@�����D�ɤޥX�Ӫ��ƾǰ��D�j�P�W�O�L���赪��D�Ѱ��D. �����ɥX���̤p����t��k, �b���ѥi�H�ΨӳB�z�έp�M�g�پǤW�譱�����D. ���O����L�o���o�M��k���ت��O���F�����@�ӤѤ�ǤW����H. �W�i�H��, �G�Q�@���e�����μƾdz��b�B�z�۵M��Ǫ����D. �b�G�Q�@�������q, �j�P�W�N�O�G���j�Ԥ���, �έp�ǻP�p�����Ǫ��ֳt�o�i, �a�ʤF���ƾdzW��, �����ƾǻP�Ͻ׳o�ǼƾǤ��䪺�o�i. �i�Ӥ]�N�ƾǪ�IJ�����J�F���|��Ǫ����. �ӹq�l�p���������, �۵M���ͤF������, �Ʀ�ƪ��s��ƧκA. �i�H��, �Ʀ�ƪ��n���P�v��, �O�̪�T�Q� � �o�ͪ�. �w��o�Ƿs����ƧκA���ͤF�s�����D, �ݭn�s����k. �o�@���s���ǰ�, �κ٬��T���B�z (signal processing). �ӳo����Ǫ��֤ߪ��@, �N�O�ť߸�1�ڦP�����k��H, ���g�O����ڪ��s�ά�Ǯa, �H�x�����J��, �ù�j�J�Τ�ƪ���s���Ұ^�m. �L�ҵo�����@��ۦW���Τ�r�d��, Rosetta stone, �b�L�Q�^����x�R�����ɭԵ��S���F, ��b�i�ܩ�j�^�ժ��]. �L��í�w����Ǯa�ͬ��l��ڳQ�y��n�j��v���p�q (1814). ���O�L�b 1807 �N�w�g����L�o�@�����ż�. �ż�. �]�N�O��, ���μƾǪ����, �q�T�ʦ �e�����z�O��, �����a�X�j, �줵���٥]�t�F�T���B�z.
�ҿ׳ť߸��ż� (Fourier series) �O��
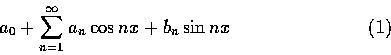
�ѩҿת��کԤ���
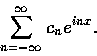
���ǯżƩM�ť߸��żƳ��O��@�Ө�Ʃ�L�a�h������k. �o�ǵL�a�h�����C�����`�O������n�Ӱ������V�ӶV�p, �i��ٲ��F�]���|�y���Ӥj��� �t. ���ǯżƧ��Ƥ��Ѧ��H�Y���I�����ߪ��h����, �ť߸��żƧ��Ƥ��Ѧ����P���W�v�i�q. ���ǯżƳq�`�u�b�Y���I������G����, �ť߸��żƳq�`�u�b�Y�Ӱ϶��������a�G����. ���ǯżƪ�������� (�p�G�s�b����), �@�w�������, �ť߸��żƪ��������, �����o�b�C���I���������.
�q (1) ���i�H�ݥX, �ť߸��żƥ��w�O�@�� ![]() �P�����.
�q�`�ڭ̥u�ݥ��b
�P�����.
�q�`�ڭ̥u�ݥ��b
![]() �������ϧ�.
�p�G�ڭ̩ҭn�B�z����� f(x) ���O��
�������ϧ�.
�p�G�ڭ̩ҭn�B�z����� f(x) ���O�� ![]() �P�����,
�q�`�ڭ̥��M�w�n�B�z���ӰϬq, ��p�� [a,b], �M��N���������Y��
�P�����,
�q�`�ڭ̥��M�w�n�B�z���ӰϬq, ��p�� [a,b], �M��N���������Y��
![]() ,
�A�N���P����, �M�����ť߸��Y��.
�D�ť߸��Y�ƪ���k, �C�b�ҥ� 637 ��.
�ҿת��P����, �N�O���Ʀb
,
�A�N���P����, �M�����ť߸��Y��.
�D�ť߸��Y�ƪ���k, �C�b�ҥ� 637 ��.
�ҿת��P����, �N�O���Ʀb
![]() ���ϧ�,
�����ۨ�
���ϧ�,
�����ۨ�
![]() ,
,
![]() ,
, ![]() �o�ǰ϶��h.
�]�N�O�w�⥦�ܦ�
�o�ǰ϶��h.
�]�N�O�w�⥦�ܦ� ![]() �P�����.
���D����
f(a) = f(b), �_�h�Q�P���Ƥ��᪺��ƬO���s��.
�P�����.
���D����
f(a) = f(b), �_�h�Q�P���Ƥ��᪺��ƬO���s��.
�Ҧp, �O
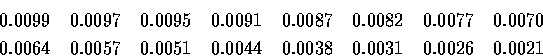
�� n �p���ɭ�, �ڭ̺� an �M bn ���C�W�Y��;
�� n �j���ɭ�, �ڭ̺� an �M bn �����W�Y��.
�q�W�����Ҥl��, �ڭ̬ݨ�, �C�W�Y�� (�������) ����j, �Ӱ��W�Y�Ƥ���p.
���o�O�Ӥ@��ʪ���H: ������ (�q�`�Ҽ���@���T��), ��C�W�����O������n��,
�Ӱ��W���������T�ܤp.2#53#>
(1) �ӥB, �ҿת����T�q�`�X��b���W����. (2) �ڭ̤]�i�H�o�˲z��:
�y�����W�һݭn����q����j, �p�G�@�@�u�������h����q,
���M��q�|�����b�C�W������.
�o��``���W�Y�ƫܤp''����H, �i�H�q�ϧΤW�[��.
���Q�@�� ![]() �P����� f(x), �b
�P����� f(x), �b
![]() ��, ��ϧΦp�U:
�Ϥ��Q�C�M���Q�K���O�O
��, ��ϧΦp�U:
�Ϥ��Q�C�M���Q�K���O�O
![]() �M
�M
![]() ���ϧ�.
���ϧ�.
![]() �O���Ϥ� y �b�W�誺���n��h�U�誺���n,
��w�n���Ȥj���O -2.5203.
�O���Ϥ� y �b�W�誺���n��h�U�誺���n,
��w�n���Ȥj���O -2.5203.
![]() �h�O�k�Ϥ� y �b�W�誺���n��h�U�誺���n,
�ѹϥi���W�U�����X�G���ۮ��h, �ҥH���ӫܤp;
��w�n���Ȥj���O 0.0516.
�h�O�k�Ϥ� y �b�W�誺���n��h�U�誺���n,
�ѹϥi���W�U�����X�G���ۮ��h, �ҥH���ӫܤp;
��w�n���Ȥj���O 0.0516.
�H�@�i�H����Ӭ���, ����q���x� �λ�X���ӤH�O��, �ݩ�C�W����. �n�ƼƥL�������X��������, �Y�W���X���վv, �ݩ��W����. �����n���������q (����Q���Ӭ۾�, ����Q���R� ���), � ���㲳o�ǰ��W. �ӧY�ϨS���o�ǰ��W, �]�ä��v�T�ڭ̿��ѳo�i�Ӥ�.
�@�� ![]() �P����ƪ���q, �M�����O�b�U�W�v�i�q����q,
�w�q�b�ҥ��� 641 ��.
�ҿ��W�Ф��R�N�O�˵��@�Ө�Ʀb�U�W�v�i�q����q.
�ڭ̬ݨ�, ���W����q�`�O�����s, �_�h���ƥ��㦳�L�a����q
(���O, �ڭ̻���۵M�ɤ����ӨS���L�a��q���T��).
�ҥ������t�F�p����W�Ф��R�Ӥ���ݲéM�p��z������.
�P����ƪ���q, �M�����O�b�U�W�v�i�q����q,
�w�q�b�ҥ��� 641 ��.
�ҿ��W�Ф��R�N�O�˵��@�Ө�Ʀb�U�W�v�i�q����q.
�ڭ̬ݨ�, ���W����q�`�O�����s, �_�h���ƥ��㦳�L�a����q
(���O, �ڭ̻���۵M�ɤ����ӨS���L�a��q���T��).
�ҥ������t�F�p����W�Ф��R�Ӥ���ݲéM�p��z������.
�ť߸��żƦp����, �i�H���O�Q�E�@�����̥D�n�ƾǰ��D���@.
���]�O�a�ʤF�ƾǤ��R���o�i�������Y���@.
�ڭ̥u���@��²�檺���p.
![\begin{displaymath}\vbox{\hsize 4.5truein\kai
�p�G $f(x)$ �b $[-\pi, \pi]$ ���s�...
...h��ť߸��żƦ���, �ӥB������Ʀb $(-\pi, \pi)$ ���������.
}\end{displaymath}](img19.gif)
26.1 �ҥ� 10.6 ���D 1-4.
26.2 �ҥ� 10.6 ���D 6, 7.
26.3 �ҥ� 10.6 ���D 19.
26.4 �ҥ� 10.6 ���D 25, 27.
;''