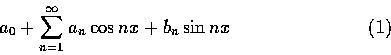
=epsf.tex
¶Ç²ÎªºÀ³¥Î¼Æ¾Ç, «üªº¬O±N¼Æ¾ÇÀ³¥Î¦bª«²z¤è±. ¨ä¹ê³o¤]¬O¤û¹y, ¼Ú©Ô³o¨Ç¦´Áªº¤Hª«©Ò±Mª`ªº°ÝÃD. ³o¤@Ãþ°ÝÃD¾É¤Þ¥X¨Óªº¼Æ¾Ç°ÝÃD¤jP¤W¬O·L¤À¤èµªº¨D¸Ñ°ÝÃD. °ª´µ¾É¥Xªº³Ì¤p¥¤è®t¤èªk, ¦b¤µ¤Ñ¥i¥H¥Î¨Ó³B²z²Îp©M¸gÀپǤW¤è±ªº°ÝÃD. ¦ý¬O·íªì¥Lµo©ú³o®M¤èªkªº¥Øªº¬O¬°¤F±À´ú¤@ӤѤå¾Ç¤Wªº²¶H. °ò¥»¤W¥i¥H»¡, ¤G¤Q¥@¬ö«eªºÀ³¥Î¼Æ¾Ç³£¦b³B²z¦ÛµM¬ì¾Çªº°ÝÃD. ¦b¤G¤Q¥@¬öªº¤¤¬q, ¤jP¤W´N¬O¤G¦¸¤j¾Ô¤§«á, ²Îp¾Ç»Ppºâ¾÷¬ì¾Çªº§Ö³tµo®i, ±a°Ê¤F¹³¼Æ¾Ç³W¹º, Â÷´²¼Æ¾Ç»P¹Ï½×³o¨Ç¼Æ¾Ç¤À¤äªºµo®i. ¶i¦Ó¤]±N¼Æ¾ÇªºÄ²¨¤¦ù¤J¤FªÀ·|¬ì¾Çªº»â°ì. ¦Ó¹q¤lpºâ¾÷ªºÀ³¥Î, ¦ÛµM²£¥Í¤FÂ÷´²ªº, ¼Æ¦ì¤Æªº·s¸ê®Æ§ÎºA. ¥i¥H»¡, ¼Æ¦ì¤ÆªºÁnµ»P¼v¹³, ¬O³Ìªñ¤T¤Q¦ ¤ µo¥Íªº. °w¹ï³o¨Ç·sªº¸ê®Æ§ÎºA²£¥Í¤F·sªº°ÝÃD, »Ýn·sªº¤èªk. ³o¤@ªù·sªº¾Ç°Ý, ²ÎºÙ¬°°T¸¹³B²z (signal processing). ¦Ó³oªù¬ì¾Çªº®Ö¤ßª«¥ó¤§¤@, ´N¬O³Å¥ß¸1¨Ú¦P´Áªºªk°ê¤H, ´¿¸g¬O®³¯¨Úªº±s¥Î¬ì¾Ç®a, ÀHx»·©º®J¤Î, ¨Ã¹ï¥j®J¤Î¤å¤Æªº¬ã¨s¦³©Ò°^Äm. ¥L©Òµo±¸ªº¤@¥óµÛ¦W«´§Î¤å¦rªdª©, Rosetta stone, ¦b¥L³Q^°ê®üx«R¸¸ªº®ÉÔµ¹¨S¦¬¤F, ²¦b®i¥Ü©ó¤j^³Õª«À]. ¥LªºÃ©wªº¬ì¾Ç®a¥Í¬¡©l©ó®³¯¨Ú³Q¬y©ñ«n¤j¦è¬vªº¤p®q (1814). ¦ý¬O¥L¦b 1807 ´N¤w¸g´£¨ì¹L³o¤@Ãþªº¯Å¼Æ. ¯Å¼Æ. ¤]´N¬O»¡, À³¥Î¼Æ¾Çªº»â°ì, ±q¤T¦Ê¦ «eªºª«²z¤O¾Ç, º¥º¥¦aÂX¤j, ¨ì¤µ¤ÑÁÙ¥]§t¤F°T¸¹³B²z.
©Ò¿×³Å¥ß¸¯Å¼Æ (Fourier series) ¬O«ü
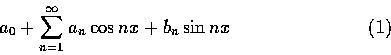
¥Ñ©Ò¿×ªº¼Ú©Ô¤½¦¡
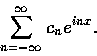
®õ°Ç¯Å¼Æ©M³Å¥ß¸¯Å¼Æ³£¬O§â¤@Ó¨ç¼Æ©î¦¨µL½a¦h¶µªº¤èªk. ³o¨ÇµL½a¦h¶µªº§C¦¸¶µÁ`¬O¤ñ¸û«n¦Ó°ª¦¸¶µ¶V¨Ó¶V¤p, ¥i¯à¬Ù²¤¤F¤]¤£·|³y¦¨¤Ó¤jªº» ®t. ®õ°Ç¯Å¼Æ§â¨ç¼Æ¤À¸Ñ¦¨¥H¬YÓÂI¬°¤¤¤ßªº¦h¶µ¦¡, ³Å¥ß¸¯Å¼Æ§â¨ç¼Æ¤À¸Ñ¦¨¤£¦PªºÀW²vªi¬q. ®õ°Ç¯Å¼Æ³q±`¥u¦b¬YÓÂIªºªþªñ¹Gªñ¨ç¼Æ, ³Å¥ß¸¯Å¼Æ³q±`¥u¦b¬YӰ϶¡¤º¥§¡¦a¹Gªñ¨ç¼Æ. ®õ°Ç¯Å¼Æªº·¥¨ç¼Æ (¦pªG¦s¦bªº¸Ü), ¤@©wµ¥©óì¨ç¼Æ, ³Å¥ß¸¯Å¼Æªº·¥¨ç¼Æ, ¤£¨£±o¦b¨CÓÂI³£µ¥©óì¨ç¼Æ.
±q (1) ¦¡¥i¥H¬Ý¥X, ³Å¥ß¸¯Å¼Æ¥²©w¬O¤@Ó ![]() ©P´Á¨ç¼Æ.
³q±`§ÚÌ¥u¬Ý¥¦¦b
©P´Á¨ç¼Æ.
³q±`§ÚÌ¥u¬Ý¥¦¦b
![]() ¤§¶¡ªº¹Ï§Î.
¦pªG§ÚÌ©Òn³B²zªº¨ç¼Æ f(x) ¤£¬OÓ
¤§¶¡ªº¹Ï§Î.
¦pªG§ÚÌ©Òn³B²zªº¨ç¼Æ f(x) ¤£¬OÓ ![]() ©P´Á¨ç¼Æ,
³q±`§ÚÌ¥ý¨M©wn³B²zþӰϬq, ¤ñ¦p»¡ [a,b], µM«á±N¤§¥²¾©ÔÁY¨ì
©P´Á¨ç¼Æ,
³q±`§ÚÌ¥ý¨M©wn³B²zþӰϬq, ¤ñ¦p»¡ [a,b], µM«á±N¤§¥²¾©ÔÁY¨ì
![]() ,
¦A±N¥¦©P´Á¤Æ, µM«á¨ú¨ä³Å¥ß¸«Y¼Æ.
¨D³Å¥ß¸«Y¼Æªº¤èªk, ¦C¦b½Ò¥» 637 ¶.
©Ò¿×ªº©P´Á¤Æ, ´N¬O§â¨ç¼Æ¦b
,
¦A±N¥¦©P´Á¤Æ, µM«á¨ú¨ä³Å¥ß¸«Y¼Æ.
¨D³Å¥ß¸«Y¼Æªº¤èªk, ¦C¦b½Ò¥» 637 ¶.
©Ò¿×ªº©P´Á¤Æ, ´N¬O§â¨ç¼Æ¦b
![]() ªº¹Ï§Î,
¤À¤ù§Û¨ì
ªº¹Ï§Î,
¤À¤ù§Û¨ì
![]() ,
,
![]() ,
, ![]() ³o¨Ç°Ï¶¡¥h.
¤]´N¬Oµw§â¥¦Åܦ¨
³o¨Ç°Ï¶¡¥h.
¤]´N¬Oµw§â¥¦Åܦ¨ ![]() ©P´Á¨ç¼Æ.
°£«Dì¨ç¼Æ
f(a) = f(b), §_«h³Q©P´Á¤Æ¤§«áªº¨ç¼Æ¬O¤£³sÄòªº.
©P´Á¨ç¼Æ.
°£«Dì¨ç¼Æ
f(a) = f(b), §_«h³Q©P´Á¤Æ¤§«áªº¨ç¼Æ¬O¤£³sÄòªº.
¨Ò¦p, ¥O
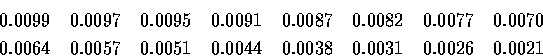
·í n ¤pªº®ÉÔ, §Ú̺٠an ©M bn ¬°§CÀW«Y¼Æ;
·í n ¤jªº®ÉÔ, §Ú̺٠an ©M bn ¬°°ªÀW«Y¼Æ.
±q¤W±ªº¨Ò¤l¸Ì, §Ú̬ݨì, §CÀW«Y¼Æ (ªºµ´¹ïÈ) ¤ñ¸û¤j, ¦Ó°ªÀW«Y¼Æ¤ñ¸û¤p.
¨ä¹ê³o¬OÓ¤@¯ë©Êªº²¶H: ¥ô¦ó¨ç¼Æ (³q±`¦Ò¼°µ¤@µ§°T¸¹), ¨ä§CÀW³¡¤À¬O¤ñ¸û«nªº,
¦Ó°ªÀW³¡¤Àªº®¶´T«Ü¤p.2#53#>
(1) ¦Ó¥B, ©Ò¿×ªºÂø°T³q±`¥X²¦b°ªÀW³¡¤À. (2) §Ṳ́]¥i¥H³o¼Ë²z¸Ñ:
³y¦¨°ªÀW©Ò»Ýnªº¯à¶q¤ñ¸û¤j, ¦pªG¤@¦@¥u¦³¦³¦hªº¯à¶q,
·íµM¯à¶q·|¶°¤¤¦b§CÀWªº³¡¤À.
³oÓ``°ªÀW«Y¼Æ«Ü¤p''ªº²¶H, ¥i¥H±q¹Ï§Î¤WÆ[¹î.
°²·Q¤@Ó ![]() ©P´Á¨ç¼Æ f(x), ¦b
©P´Á¨ç¼Æ f(x), ¦b
![]() ¤¤, ¨ä¹Ï§Î¦p¤U:
¹Ï¤¤Q¤C©M¤¤Q¤K¤À§O¬O
¤¤, ¨ä¹Ï§Î¦p¤U:
¹Ï¤¤Q¤C©M¤¤Q¤K¤À§O¬O
![]() ©M
©M
![]() ªº¹Ï§Î.
ªº¹Ï§Î.
![]() ¬O¥ª¹Ï¤¤ y ¶b¤W¤èªº±¿n´î¥h¤U¤èªº±¿n,
¨ä©w¿n¤ÀȤj¬ù¬O -2.5203.
¬O¥ª¹Ï¤¤ y ¶b¤W¤èªº±¿n´î¥h¤U¤èªº±¿n,
¨ä©w¿n¤ÀȤj¬ù¬O -2.5203.
![]() «h¬O¥k¹Ï¤¤ y ¶b¤W¤èªº±¿n´î¥h¤U¤èªº±¿n,
¥Ñ¹Ï¥i¨£¤W¤U³¡¥÷´X¥G¤¬¬Û®ø¥h, ©Ò¥HÀ³¸Ó«Ü¤p;
¨ä©w¿n¤ÀȤj¬ù¬O 0.0516.
«h¬O¥k¹Ï¤¤ y ¶b¤W¤èªº±¿n´î¥h¤U¤èªº±¿n,
¥Ñ¹Ï¥i¨£¤W¤U³¡¥÷´X¥G¤¬¬Û®ø¥h, ©Ò¥HÀ³¸Ó«Ü¤p;
¨ä©w¿n¤ÀȤj¬ù¬O 0.0516.
¥H¤@±i¤H¹³ªñ·Ó¬°¨Ò, ¯à°÷±q¤©x¥ §Î»¥X¨ºÓ¤H¬O½Ö, ÄÝ©ó§CÀW³¡¤À. n¼Æ¼Æ¥L²´¨¤¦³´Xµ·³½§À¯¾, ÀY¤W¦³´X²ô¥Õ¾v, ÄÝ©ó°ªÀW³¡¤À. ¥²¶·n¤ñ¸û°ªªº¯à¶q (¤ñ¸û¶Qªº·Ó¬Û¾÷, ¤ñ¸û¶Qªº¨R¬ µ§Ç), ¤ ¯àÅã²³o¨Ç°ªÀW. ¦Ó§Y¨Ï¨S¦³³o¨Ç°ªÀW, ¤]¨Ã¤£¼vÅT§ÚÌ¿ëÃѳo±i·Ó¤ù.
¤@Ó ![]() ©P´Á¨ç¼Æªº¯à¶q, ©M¥¦¤À§O¦b¦UÀW²vªi¬qªº¯à¶q,
©w¸q¦b½Ò¥»ªº 641 ¶.
©Ò¿×ÀWÃФÀªR´N¬OÀ˵ø¤@Ó¨ç¼Æ¦b¦UÀW²vªi¬qªº¯à¶q.
§Ú̬ݨì, °ªÀWªº¯à¶qÁ`¬Oº¥´î¨ì¹s, §_«hì¨ç¼Æ¥²¨ã¦³µL½aªº¯à¶q
(¦ý¬O, §ÚÌ»¬°¦ÛµM¬É¤¤À³¸Ó¨S¦³µL½a¯à¶qªº°T¸¹).
½Ò¥»¤¤ªíºt¤F¦p¦ó¥ÎÀWÃФÀªR¨Ó¤À¿ë½Ý²Ã©M¤p³â¥zªºµ¦â.
©P´Á¨ç¼Æªº¯à¶q, ©M¥¦¤À§O¦b¦UÀW²vªi¬qªº¯à¶q,
©w¸q¦b½Ò¥»ªº 641 ¶.
©Ò¿×ÀWÃФÀªR´N¬OÀ˵ø¤@Ó¨ç¼Æ¦b¦UÀW²vªi¬qªº¯à¶q.
§Ú̬ݨì, °ªÀWªº¯à¶qÁ`¬Oº¥´î¨ì¹s, §_«hì¨ç¼Æ¥²¨ã¦³µL½aªº¯à¶q
(¦ý¬O, §ÚÌ»¬°¦ÛµM¬É¤¤À³¸Ó¨S¦³µL½a¯à¶qªº°T¸¹).
½Ò¥»¤¤ªíºt¤F¦p¦ó¥ÎÀWÃФÀªR¨Ó¤À¿ë½Ý²Ã©M¤p³â¥zªºµ¦â.
³Å¥ß¸¯Å¼Æ¦p¦ó¦¬ÀÄ, ¥i¥H»¡¬O¤Q¤E¥@¬öªº³Ì¥Dn¼Æ¾Ç°ÝÃD¤§¤@.
¥¦¤]¬O±a°Ê¤F¼Æ¾Ç¤ÀªRªºµo®iªº¤õ¨®ÀY¤§¤@.
§ÚÌ¥u»¡¤@ºØ²³æªºª¬ªp.
![\begin{displaymath}\vbox{\hsize 4.5truein\kai
¦pªG $f(x)$ ¦b $[-\pi, \pi]$ ¤¤³sÄ...
...h¨ä³Å¥ß¸¯Å¼Æ¦¬ÀÄ, ¦Ó¥B·¥¨ç¼Æ¦b $(-\pi, \pi)$ ¤¤µ¥©óì¨ç¼Æ.
}\end{displaymath}](img19.gif)
26.1 ½Ò¥» 10.6 ²ßÃD 1-4.
26.2 ½Ò¥» 10.6 ²ßÃD 6, 7.
26.3 ½Ò¥» 10.6 ²ßÃD 19.
26.4 ½Ò¥» 10.6 ²ßÃD 25, 27.
;''