![]() Page 159
Line 1 - 2
Page 159
Line 1 - 2
![]() 因此
因此
![]() ,
,
![]() 。
這麼一來,就連方盒函數都不在 V0 裡面了,這會給我們許多不必要的限制。
所以我們要求
。
這麼一來,就連方盒函數都不在 V0 裡面了,這會給我們許多不必要的限制。
所以我們要求
![]() Page 159
Line 10
Page 159
Line 10
![]() 必要的條件。以後會明白,沒有了這個
必要的條件。以後會明白,沒有了這個 ![]()
![]() Page 167
Line 13
Page 167
Line 13
是,若挑定一個很大的 j,則
![]() 的函蓋寬度幾乎是 0;
我們很難
的函蓋寬度幾乎是 0;
我們很難 ![]()
![]() Page 168
Line -5 - -3
Page 168
Line -5 - -3
反過來,若 ![]() ,則
,則
![]() 所以
所以 ![]() 或
或 ![]() 。由於
。由於
![]() 是 V1 的基底,故存在 vk 使得
是 V1 的基底,故存在 vk 使得
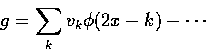
![]() Page 173
Line 7 - 10
Page 173
Line 7 - 10
將上式中的和分成奇數與偶數兩半來做,就發現
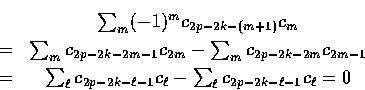
![]() Page 213
Line -3 - -2
Page 213
Line -3 - -2
![]() 前式之第一項為 0。
故
前式之第一項為 0。
故
![]() 。
再由 Parseval 等式得
。
再由 Parseval 等式得
![]() Page 223
Line 1
Page 223
Line 1
回顧
![]() ,
根據 (2.51) 和 (2.44),
,
根據 (2.51) 和 (2.44),
![]() Page 224
Line -6 - -5
Page 224
Line -6 - -5
性質 3.4 若
![]() 且 (3.63) 中定義的
且 (3.63) 中定義的
![]() 為連續之
為連續之 ![]() 週期函數。
則
週期函數。
則
![]() 形成一個正則函數集合的充分且必要條件是
形成一個正則函數集合的充分且必要條件是