數學素養教育

因式分解不是為了訓練邏輯思考

西元 2020 年 9 月底，「中學數學課程」一位同學提問：

在我大四那年教補習班曾經被學生問說：老師，這個單元好難，學了可以幹嘛？ 我有點忘記，當時好像是因式分解單元。 記得當時對學生說，這個以後用不到，除非你們以後走理工相關科系才會繼續碰到。 接著，我對學生說，學數學不是一直在算數，而是訓練你的邏輯思考能力。 請問單老師，當時我對學生的回答是否恰當？或有沒更好的回應方式？

我個人的願望是：願天下數學老師不要再這樣說了。

數學的學習過程，可能發生一些有助於「心理素質」的「副作用」， 包括很多人說的「邏輯思維」、「運算思維」。 徐光啟也有類似言論，他說的優異心理素質是「縝密」： 心思「縝密」就是比較不容易有漏洞，能為問題提出思慮周延的解決方案。 相信許多數學系學生有此同感。

也有不少人認為，數學還能增強一個人的「恆毅力」： 不怕挫折而長時間努力於一件沒有立即回報的工作。 最後這一點，可能也有道理，但是我卻不免感到啼笑皆非。

但是數學教育的價值，不可以只有上述「副作用」。 原因有二。

1. 其他學科也可能具備同樣的效果。 例如程式設計更直接地鍛鍊邏輯思維，體育或音樂、美勞也可能鍛鍊恆毅力； 只要有過拉小提琴的挫折經驗，就不難體會音樂帶來的恆毅鍛鍊。 哲學或辯論也可以鍛鍊思考的縝密性。 所以，如果數學的價值只有這些，它就可以隨時被其他學科取代。 而我們應該知道，數學有其不可被取代的價值， 我們要教好那些價值，而不該著重在「副作用」。 例如，如果要鍛鍊邏輯思維， 肯定有比做因式分解更有效、更直接，而且更不「白白受苦」的方法； 例如練習寫程式。
2. 學習心理學者已經大致上有此共識： 學習 A 而獲得能力 B 的想法，基本上是錯誤的。 例如有人認為彈鋼琴會提升數理能力，聽音樂會提高智商（特別是聽莫札特的音樂）， 這些想法，基本上就像相信吃核桃會補腦、吃虎鞭會壯陽一樣， 沒有實證的效果。

所以，請不要再用「邏輯」、「思考」當作學習數學的理由了。 學習數學就是因為「數學有用」而且我們「需要數學」。

以「因式分解」為例，讓我們先約定一個「潛規則」： 只做有理係數（甚至整係數）的因式分解。 例如在中學通常不討論 \(x^2-2=(x+\sqrt2)(x-\sqrt2)\) 這種因式分解。

在學校課程中，因式分解的「存在理由」（reason to be）是多項式等式的求解方法之一， 特別是俗稱「二次方程」的求解方法。 到了高中，搭配所謂「有理根檢驗法」，因式分解也用來求解三次或四次方程。 讀者應該要明白的是：在真實世界中，人們幾乎從來不會用因式分解來求方程的解。 原因很明顯：

1. 真實世界裡發生的方程，很少是整係數的。當然，有理係數都可以整理成整係數， 但在實用的程序裡，並不會刻意將方程整理成整係數。 以基本的自由拋射為例，二次項通常都是 \(-4.9x^2\)，非整係數。
2. 即使是整係數方程，也不一定會有「有理根」。事實上，任意創造一個二次方程， 發生有理根的機率是：零。

那麼，因式分解的「存在理由」究竟是什麼呢？ 在高深的數學論證中，或許會遇上它， 那些數學也可能出現在電機、電子、資工的專業領域中； 但它們都是非常特殊的用途， 實在不構成中學生都該學習因式分解的理由。 在數學發展史中，因式分解的「存在理由」是做多項式分式的「分項分式」， 它是為有理函數找反導函數的根本方法。 而且，此時並不侷限於有理係數的分解，只要是實係數即可。例如 \[{1\over x^2-2}={\sqrt2\over4}\left({1\over x-\sqrt2}-{1\over x+\sqrt2}\right)\]

前面說過實際上並不會用因式分解來求方程的解， 在中學課程裡，為了方便舉例， 教學與練習的操作總是設計具有「有理根」的題目讓學生做， 確實是個「無可厚非」的「權宜之計」。 但是教師同仁應該明白：不要誤將權宜的過程當成了目的。 因式分解本身不是目的，而是權宜的程序。 中學階段的因式分解教學目的，有以下幾點：

• 在國中二年級，教學生因式分解的最主要目的是為高中的因式定理做準備。 例如，國中生要明白為何將 \(x^2-2x=8\) 分解成 \(x(x-2)=8\) 無濟於事？
• 到了國中三年級，藉因式分解讓學生理解二次方程的「解」和二次函數的「根」， 以及二次函數圖形與 x 軸的交點，三者之間的關係。
• 在高中一年級，教學目的是藉因式分解了解除法原理、因式定理、餘式定理。 學生還要明白，在實係數中，不可分解式的最高可能次數為二次。 過度操作有理根檢定是無關宏旨的，因為前面說過：實際上發生有理根的機率是零。

如果明白以上三項教學目標，並且依據它們來安排因式分解的教學例與評量試題， 就應該知道不需要過度練習。在合理的國中需求下，國中程度的學生應該不至於因為太困難而質疑「為什麼要學因式分解」？ 即使有學生問了，只要教師的佈題確實吻合教學目標，也就可以明白告訴學生學習的理由了。

什麼是過度練習？以下舉出幾個例子。歡迎讀者來信分享更多「反例」。

1. \( x^2+y^3+xy^2+2xy-1\)
2. \(x^4-4y^4-4xy^3-x^2y^2\)
3. \(a^4+a^2-2ab-b^2+1\)
4. \(x^3+y^3+z^3-3xyz\)

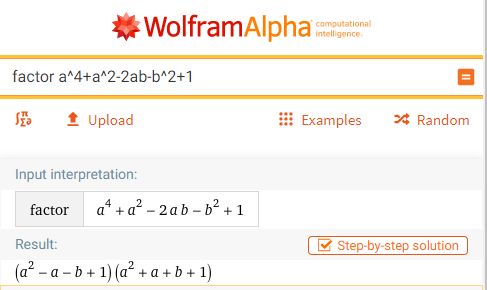
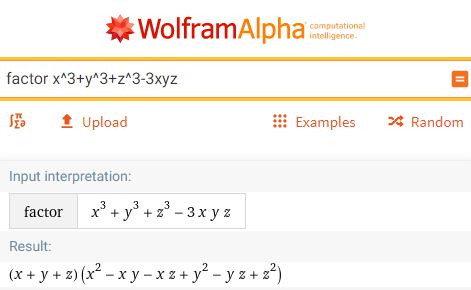
當然，因式分解在未來的用途還有無限可能，只是我們現在還不知道。 可是，即使將來有一天因式分解變得非常重要，也不必擔心， 因為今天已經具備非常成熟的電腦軟體：電腦代數系統 (Computer Algebra System, CAS)， 可以輕易幫我們做因式分解。 CAS 曾經所費不貲，可是隨著科技進步，它們已經出現免費的網頁版了。 例如著名的 Wolfram Alpha 就能做因式分解。 我用前面的最後兩題為例，展示給讀者看：

   

因為有理函數的反導函數也同樣被 CAS 軟體解決了，所以學習微積分的學生， 也只要了解分項分式的原理即可。因此，大學生為了學習所需的因式分解， 還是可以限制在整係數多項式的分解。 可見不論中學還是大學，因式分解都可以僅限整係數，作為概念理解和程序練習的對象。 在國中，所有的需求只到二次為止；在高中，則需要提升到三次，有時候需要四次。

不知道會不會有人要問： 如果有一天全天下的電腦都壞了，而我們需要因式分解，怎麼辦？ 我不知道該怎樣回答這個問題。

最後，作者要強調：只要學生學得會，教什麼都是值得的。 因式分解是許多數學教授當學生時的最愛，我們都曾醉心於因式分解如「謎題」般的魔力， 以及「解謎」之後的快感。 以上發言，都是針對學生學不會的時候，最低限度的教學目標應該設在何處？ 教學示例與評量試題應該依據教學目標而有所拿捏。