我國各項措施經常跟隨在日本之後，就連企業經營方針都是的。 例如我國「大考中心」（1989 年成立）就對日本 「大學入試中心」 （大学入試センター，1977 年成立）有過相當的研究與參照。 該中心於西元 2021 年（令和三年）1 月推出第一屆「大學入學共通測驗」 （大学入学共通テスト），其改革主旨是希望能評量「學生習得什麼樣的素質能力」。 日本的大考共有四份數學科試卷，本文取其中一份作為範例，跟大家一起欣賞： 由於日本「大學入試中心」官網沒有公布 2021 年的試卷， 我從 東進 補習班網頁取得試卷，但它卻是掃描的圖檔，難以編輯。 因此，我在前面的連結提供「東進」版的原文試卷， 下文提供中文翻譯。我上次研究日本的數學課程，是在 2004-5 年間， 帶領研究生參與陳宜良教授的國際比較研究團隊。 日本的研究結果如下文，這是我對日本數學課程的基礎知識：
下文將涉及日本高中數學的四門課程：《數學Ⅰ》、《數學Ⅱ》、《數學Ａ》、《數學Ｂ》，我曾在《科學月刊》就實際的教科書簡介這些課程的內容，請看
- 洪雅齡（2005）。臺灣與日本之十二年數學課程比較。國立中央大學碩士論文。 〔全文〕
時隔兩年（2023 年 7 月），廖育萱完成「日本新舊大考數學試題比較」的碩士研究論文，她蒐集了
- 單維彰（2013）。日本高中數學課本簡報。科學月刊 102 年 7 月。 〔完稿全文〕
這次考試改革是日本文部科學省 「高大接続改革」的一環。 整個「高大接續」始自 2015 年，意思是「高中」（高等學校）與「大學」的「接續」。 這個標題下得好，言外之意就是「高中」和「大學」以前並沒有接續， 高中畢業的大學入學考試，純粹就是一道「關卡」， 「關卡」之前和「關卡」之後是兩個未必相連的世界。 打通這一關就可以進大學，可是打過這一關的本領，在過關之後卻不見得用得著。 日子久了，高中教育的目的就是為了戰勝那一關，而不在乎過關之後要怎樣？ 因為它反正是個無關的另一個世界。 「高大接續」希望新教育能讓高中學生從「受教」轉為「習得」， 而新的大學考招能夠讓高中和大學的教育「接續」。 日本文部省期許新的高中教育
必須採取旨在培養學生發現問題和解決問題能力的「主動學習」制度， 改善高中教師的素質和數量； 要改變以往在大學入學考試中偏重知識技能考察， 採用多種選擇的考試形式，向敘事型選拔方式轉變， 以評估學生思考、判斷和表達能力為重。
2015 年「高大接續」規劃的鴻圖大業， 因為政治環境變動，並未如期實施，有些改革擱置了，有些則推遲。 例如新式大考就延遲了一年，在 2021 年 1 月正式登場。 而本來要跟著「共通測驗」一起登場的「上機考」（computer-based test, CBT） 則不定期推遲；但是他們在 2021 年 3 月提出一份厚實的 CBT 研究報告， 看來此事還在準備中，並未放棄。
新版「共通測驗」仍然在每年 1 月 13 日之後的第一個週六、週日舉行； 例如 2021 年在 1 月 16 日、17 日。 「共通測驗」總共提供 6 個領域的 30 門考科，英語必須參加聽力測驗， 其他選考的外語（法、德、中、韓）則只考閱讀。 數學安排在第二天，仍然有兩段時間的考試，每段時間提供兩個考科，學生擇一作答。 新考試的第一節數學比舊考試多給 10 分鐘的時間（從 60 分鐘增加到 70 分鐘）， 但是第二節數學仍是 60 分鐘。 這兩節數學考試的四個考科都基於高一、高二的數學課程（數學Ｉ、Ⅱ 是必修， 數學Ａ、Ｂ是選修），可見「共通測驗」相當於我國的「學測」而不是「指考」。
比較新、舊兩版的試題，觀察前後的差異，應該很有趣，也應該對我們很有啟發。 可是我沒有時間翻譯全部的 8 份考卷， 謹提供日文原文試卷如下，請讀者自行瀏覽； 如果有熱心人士自願翻譯，則請自行公布譯文，或者分享給我貼在這裡也可以。
數學第一節（2020：60 分鐘，2021：70 分鐘）
數學第二節（60 分鐘）
解答用紙上若未正確填入的話將不計分。特別注意的是，若沒有在解答用紙上標記要考的是哪個科目 (解答科目欄) 或者選擇超過一個科目的話將視為零分。
接下來是作答說明，看得出來都是選填的格式（選擇題也可以包括在內）， 每一格畫一個數目字或符號，項目 2 舉例說 \(-83\) 要畫三格。 分數若為負數，負號要寫在分子。 而且，分數和根式都要化到最簡，例如 \({6\over8}\) 不可以，\(2\sqrt8\) 也不可以， 必須回答 \({3\over4}\) 和 \(4\sqrt2\)。 我認為這是很糟糕的設計，削足適履，強迫人去適應技術上的障礙。
如果答案格是長方形，表示它是選填題；如果答案格式雙重長方形，表示它是選擇題。 選擇題的選項也是用一位數字表示，0 或 1 或 2 等，最多可以有 10 個選項， 但皆為單選。 有些答案格兼具變數名的效用，它會出現不止一次。 當它第一次出現（需要作答）時，它的外框會用粗線，再度出現就用普通線。 如果只看規則，感覺頗複雜的。 可是實際閱讀題本時，感覺還蠻自然的，從前後文看得出來該是填充還是選擇。
以下只看「數學Ｉ．數學Ａ」試卷，因此從第 29 頁開始。 第 29 頁是說這份試卷有 5 大題，第 1、第 2 大題必答，後面 3 大題選 2 大題作答。
- [1] c 為正整數，① 是 x 的二次方程式 \[2x^2+(4c-3)x+2c^2-c-11=0\]
- (1) 當 \(c=1\) 的時候將 ① 做因式分解的結果若如下，x 的解為
(2) 當 \(c=2\) 的時候，① 的解如下列。較大數值的解以 a 表示， 則下式應該為多少。此外，符合此條件的整數 m 為多少。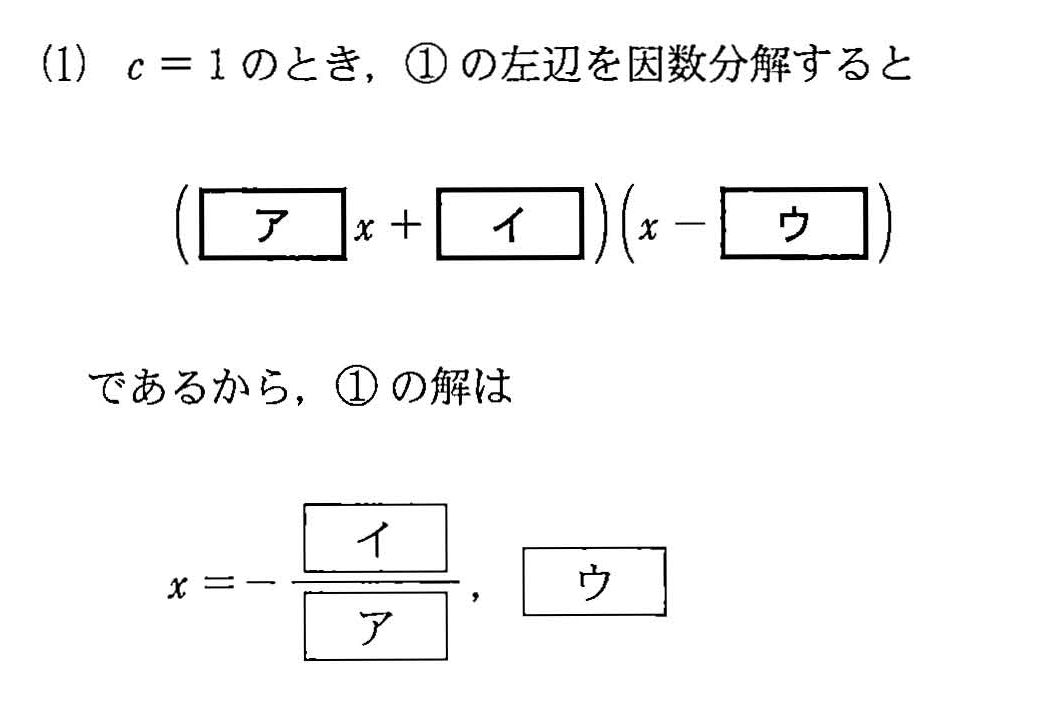
(3) 太郎跟花子在看 ① 的解。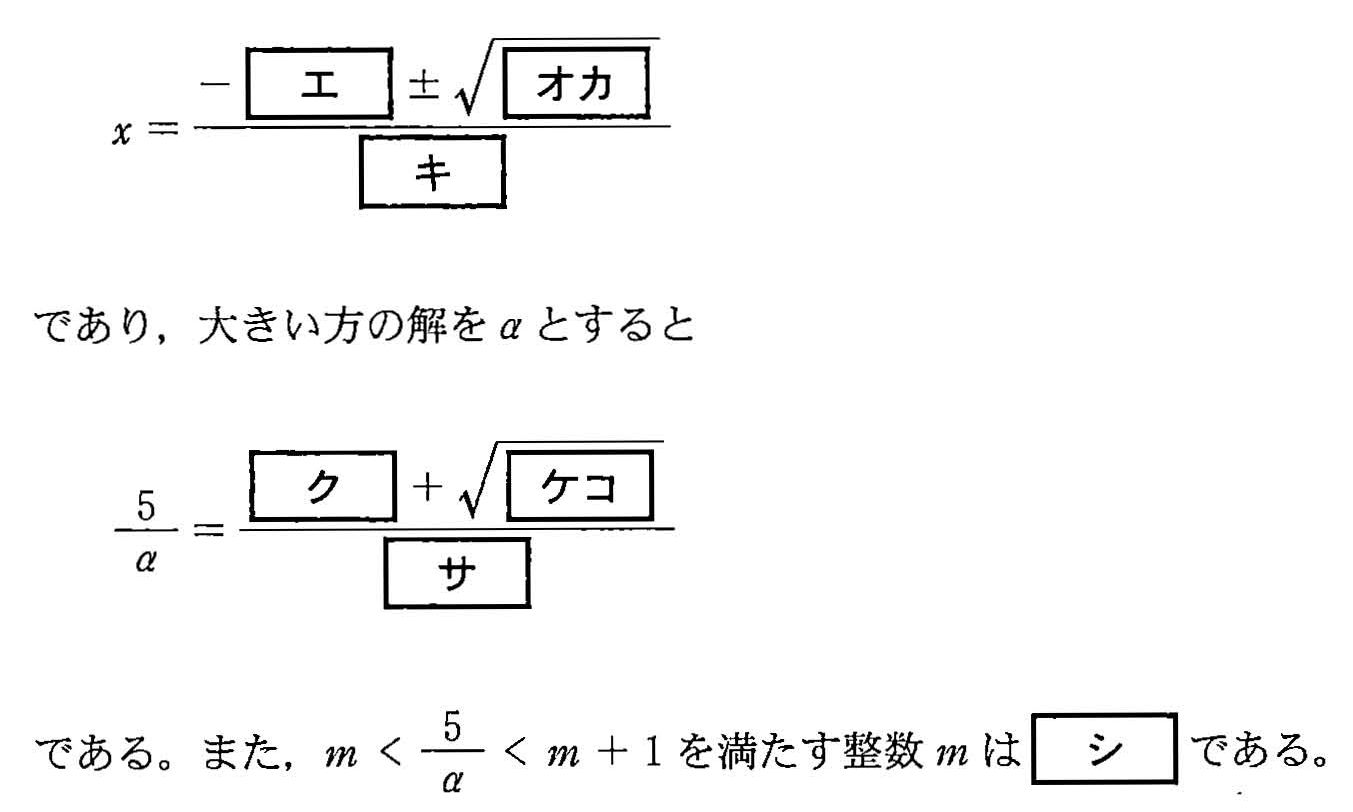
太郎：① 的解會因 c 值而異，有時候會是有理數、有時也可能是無理數呢。 c 值在什麼條件下會讓解答為有理數呢。
花子：這問題應該只要透過觀察二次方程式中根號的部分就可以知道了吧。
如上討論，會讓 ① 解出兩個不同的有理數的可能正整數 c 值共有幾個？- [2] 如圖，ΔABC 的外側分別有與 AB, BC, CA 線段共用的正方形 ADEB, BFGC, CHIA，此外 EF, FG, ID 分別有連線。下述符號定義 \[ BC=a,\quad AC=b,\quad AB=c,\quad \angle CAB=A,\quad \angle ABC=B,\quad \angle BCA=C\]
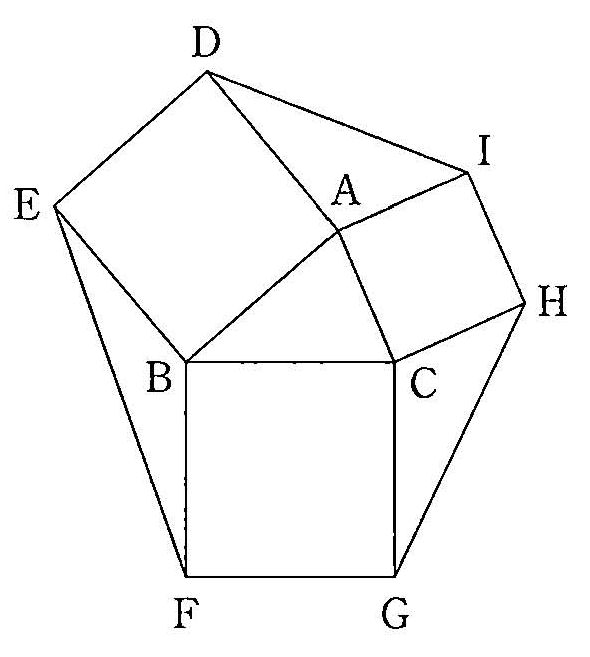
- (1) \(b=6\), \(c=5\), \(\cos A={3\over5}\) 的時候， \(\sin A\) 是多少？ΔABC 的面積是多少？ΔAID 的面積是多少？
(2) 正方形 BFGC, CHIA, ADEB 的面積依序為 \(S_1\), \(S_2\), \(S_3\)。 則關於 \(S_1-S_2-S_3\) 的值，由以下選項選出正確答案。
空格中填入以下選項：
- 當 \(0^\circ<A<90^\circ\) 時，其值 □
- 當 \(A=90^\circ\) 時，其值 □
- 當 \(90^\circ<A<180^\circ\) 時，其值 □
0. 為 0(3) ΔAID, ΔBEF, ΔCGH 的面積依序為 \(T_1\), \(T_2\), \(T_3\)。 下列選項何者正確？
1. 為正值
2. 為負值
3. 可能正也可能負0. 當 \(a<b<c\) 時，\(T_1>T_2>T_3\)(4) 以下討論 ΔABC, ΔAID, ΔBEF, ΔCGH 以及它們的外接圓半徑。
1. 當 \(a<b<c\) 時，\(T_1<T_2<T_3\)
2. 當 A 是鈍角時，\(T_1<T_2\) 且 \(T_1<T_3\)
3. 與 a, b, c 的值無關，\(T_1=T_2=T_3\)
當 \(0^\circ < A < 90^\circ\) 時，
ID □ BC 且 ΔAID 外接圓半徑 □ ΔABC 外接圓半徑。
空格中填入以下選項：0. \(<\) 1. \(=\) 2. \(>\)當 \(0^\circ < A < B < C < 90^\circ\) 時，外接圓半徑最小的是 □。
當 \(0^\circ < A < B < 90^\circ <C \) 時，外接圓半徑最小的是 □。
空格中填入以下選項：0. ΔABC 1. ΔAID 2. ΔBEF 3. ΔCGH
[1] 田徑短跑項目中，100公尺要花多久時間跑完， 與一步能跨出幾公尺 (stride) 以及每一秒可以跨出幾步 (pitch) 有很大的關係。 stride 與 pitch 的公式分別如下：
stride(m/步) = \(\displaystyle{\text{100m}\over\text{跑完 100m 需要的步數}}\)然而最後一步很有可能不是整數，此時會用小數表示。（接下來將會省略單位） 例如：總時數 10.81 秒，共計跑了 48.5 步的時候，stride 是 \({100\over48.5}\) 大約為 2.06、pitch 是 \({48.5\over10.81}\) 大約為 4.49。
pitch(m/秒) = \(\displaystyle{\text{跑完 100m 需要的步數}\over\text{總時間(秒)}}\)請注意如果答案有小數點，請依照題目要求的精準度填入四捨五入的結果。
- (1) 令 stride = x 代表每步前進的距離，pitch = z, 代表每秒的步數， 則請用 x 與 z 表示每秒前進的距離，也就是平均速度 [A] (m/秒)。 (從下面方框的解答群選出正解) 基於上述，總時間也可透過 x 和 z 表示如下。 \[ \text{總時間} = {100\over\text{[A]}} \] 因此平均速度最大的時候，就是表現最佳的時候（注意，總時間越小越好）。
0. \(x+z\) 1. \(z-x\) 2. \(xz\) 3. \(\displaystyle{x+z\over2}\) 4. \(\displaystyle{z-x\over2}\) 5. \(\displaystyle{xz\over2}\)(2) 百米競賽男子組參賽選手太郎為了爭取第一名， 正在考慮最佳的 pitch & stride 組合。 下表為太郎練習時的三種不同可能的 pitch & stride 組合。此外，每個人體能上都有 pitch & stride 各自的限制所在； 對太郎而言，stride 最高就是 2.40、pitch 則是 4.80。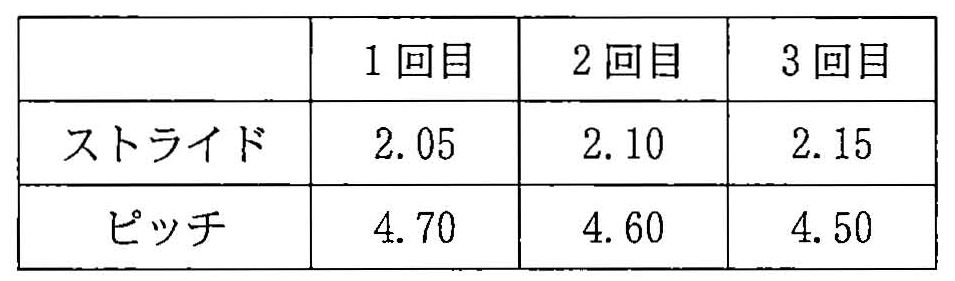
關於 pitch & stride 的相關性，對太郎來說， 每當 stride 增加 0.5 的時候 pitch 就會降低 0.1。 用二元一次方程式表達上述關聯性的話，則會如下方程式 ②： (stride=x, pitch=z)
基於太郎的 stride & pitch 的限制，x 的範圍可表示如下：
承第 (1) 題的 [A]，利用 ② 將 \(y=\text{[A]}\) 寫成 y 是 x 的函數， 再加上考慮前述的最大值限制後，即可求出 y 的最佳解。 試問當 x 為何時，y 達到最大值？
因此，太郎能跑出的最佳成績為 stride 控制在 □、ptich調整為 □的時候。 （選填，數值如同前面的 x，皆為一位整數與二位小數） 這時候，太郎的總時間根據方程式 ① 將會是以下哪個選項？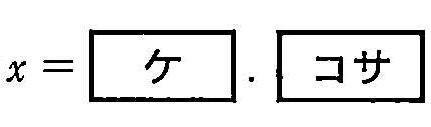
0. 9.68 1. 9.97 2. 10.09 3. 10.33 4. 10.42 5. 10.55- [2] 就業者的產業依照主教的經濟活動分為三種：第一級產業（農/林/漁）、 第二級產業（礦/建設/製造）以及第三級產業（上述以外）。 國內的就業調查結果（國勢調查）中，47 個都道府縣分別依照此三種產業分類做調查。 各行政區底下，各產業的總人數除以總就業人數的數據，稱為各產業的「就業者數比例」。
- (1) 下圖表示了從 1975 年到 2010 年，切為 8 個年度（五年一期） 各行政區三個產業的就業者數比例的盒狀圖， 各年段由上而下的方盒依序代表第一/第二/第三級產業。
根據上圖能觀察到的現象，下列有兩個選項是不正確的，分別是□和□ (答案順序不拘)。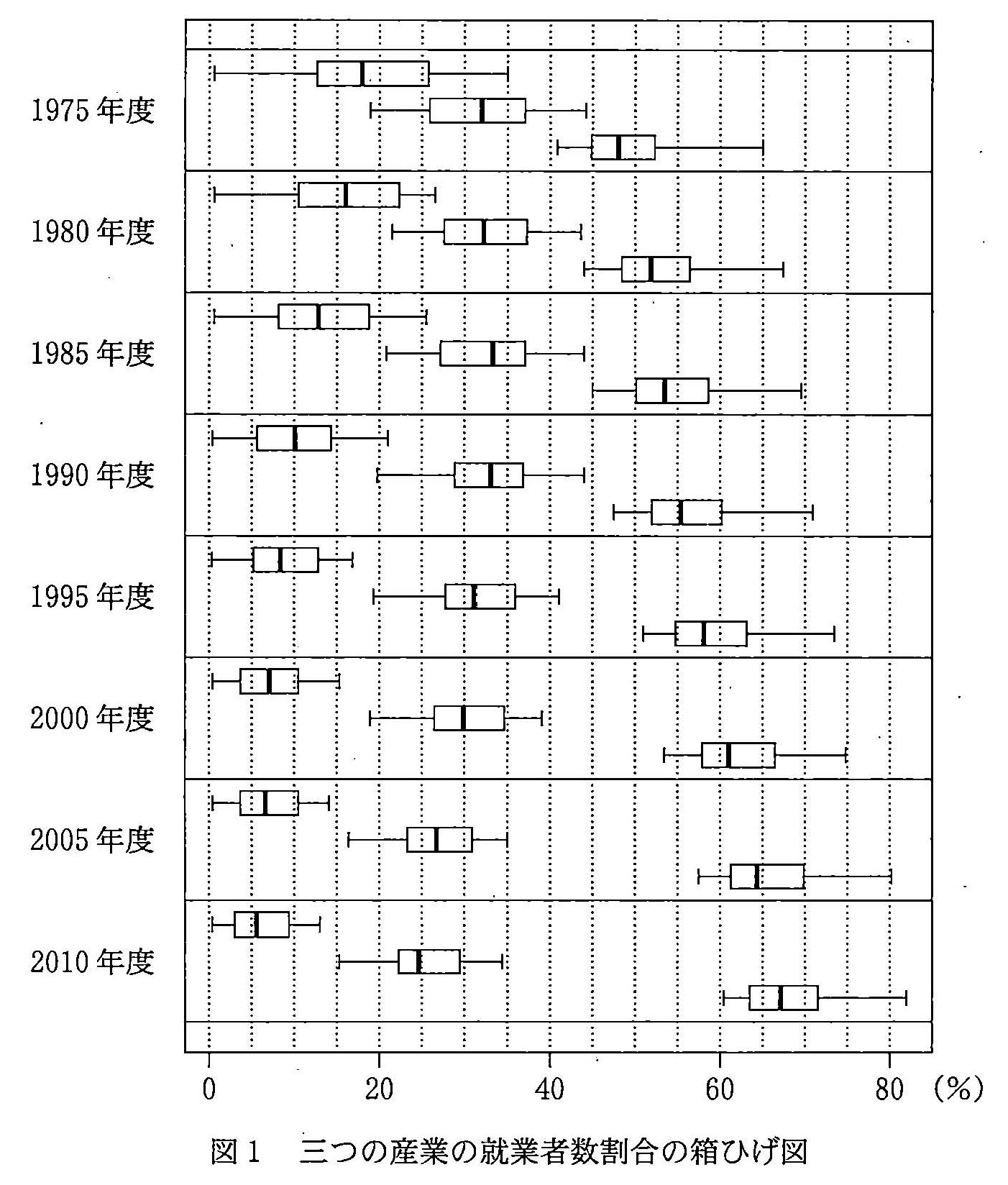
(圖出處：總務省網站資料)0. 第一級產業的就業者比例的四分位距，直至 2000 年度都呈現減少的趨勢。(2) 接下來從圖 1 取出五個時間點的資料， 針對第一級產業與第三級產業的就業者比例製造直方圖如下，左側那一叢代表第三級產業。 直方圖各區間包含左端點、不含右端點。
1. 第一級產業的就業者比例，無論哪個時間點、左鬚都比右鬚長。
2. 第二級產業的就業者比例的中間值自 1990 起呈減少的趨勢。
3. 第二級產業的就業者比例的第 1 四分位數逐年降低。
4. 第三級產業的就業者比例的第 3 四分位數逐年增加。
5. 第三級產業的就業者比例的最小值逐年增加。根據前述資訊判斷，1985 年度的圖為何？1995 年度的圖為何？ （圖的編號即為選項。）
(3) 將三種不同產業兩兩捉對製作散佈圖如下。 圖 2 從左到右是為 1975 年度的第一級、第二級、第三級產業， 圖 3 則為 2015 年度。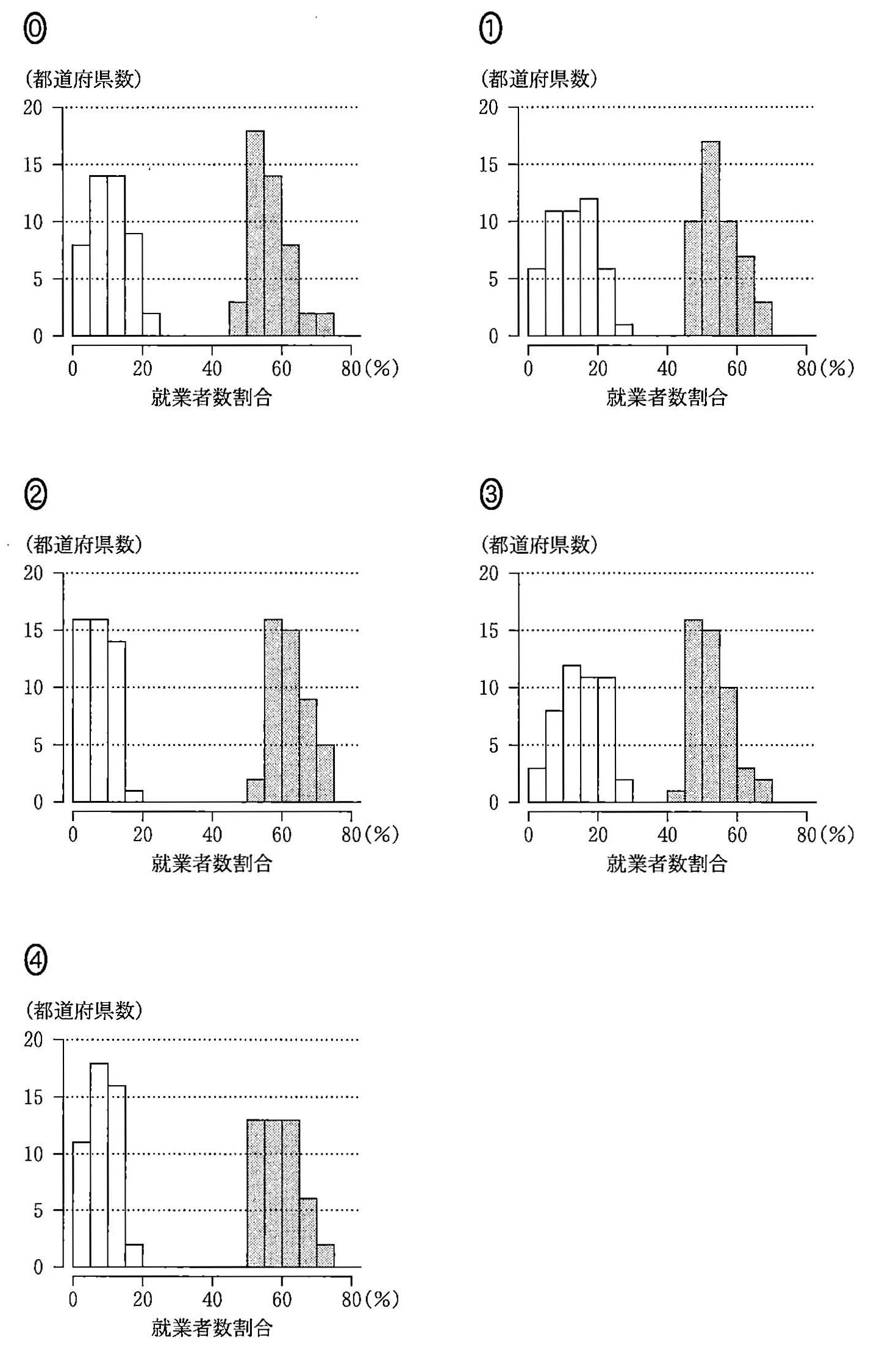
(圖出處：總務省網站資料)下列三條評論是著眼於 2015 年相對於 1975 年的變化的描述。 在此處「相關性變高」的意思為相關係數的絕對值較大。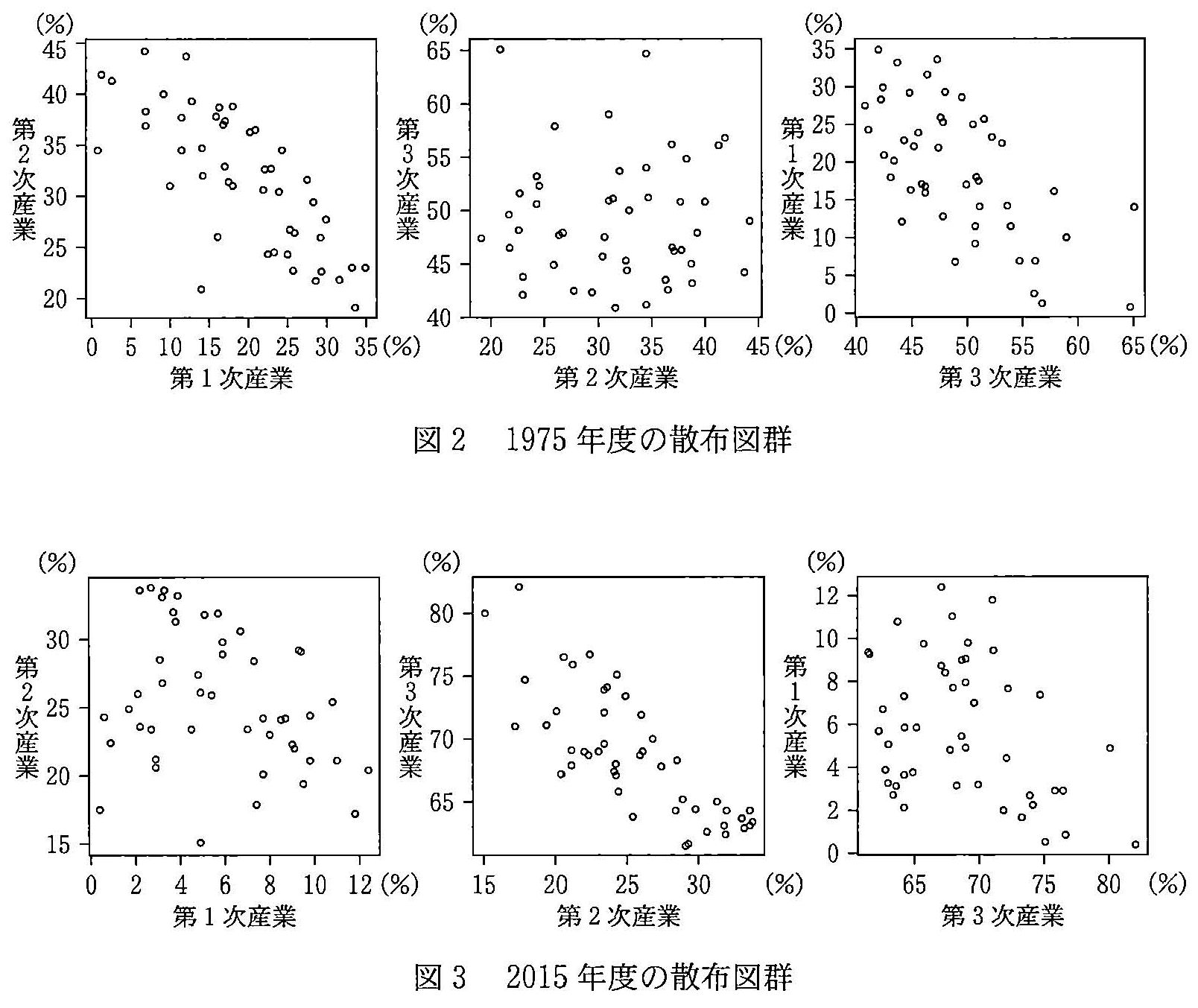
(圖出處：總務省網站資料)上述內容正確與否的結果為何？（從下方表格選擇）
- 各行政區的第一級產業的就業比例與第二級產業的就業比例的相關性變高了。
- 各行政區的第二級產業的就業比例與第三級產業的就業比例的相關性變高了。
- 各行政區的第三級產業的就業比例與第一級產業的就業比例的相關性變高了。
(4) 以下針對就業者再以性別做區分。 此處將以「男性就業比例」和「女性就業比例」 表示該行政區中某性別就業人數除以總就業人數的比例。 下圖描繪了 2015 年度第一級產業就業者（橫軸）與男性就業比例（縱軸）的散佈圖。
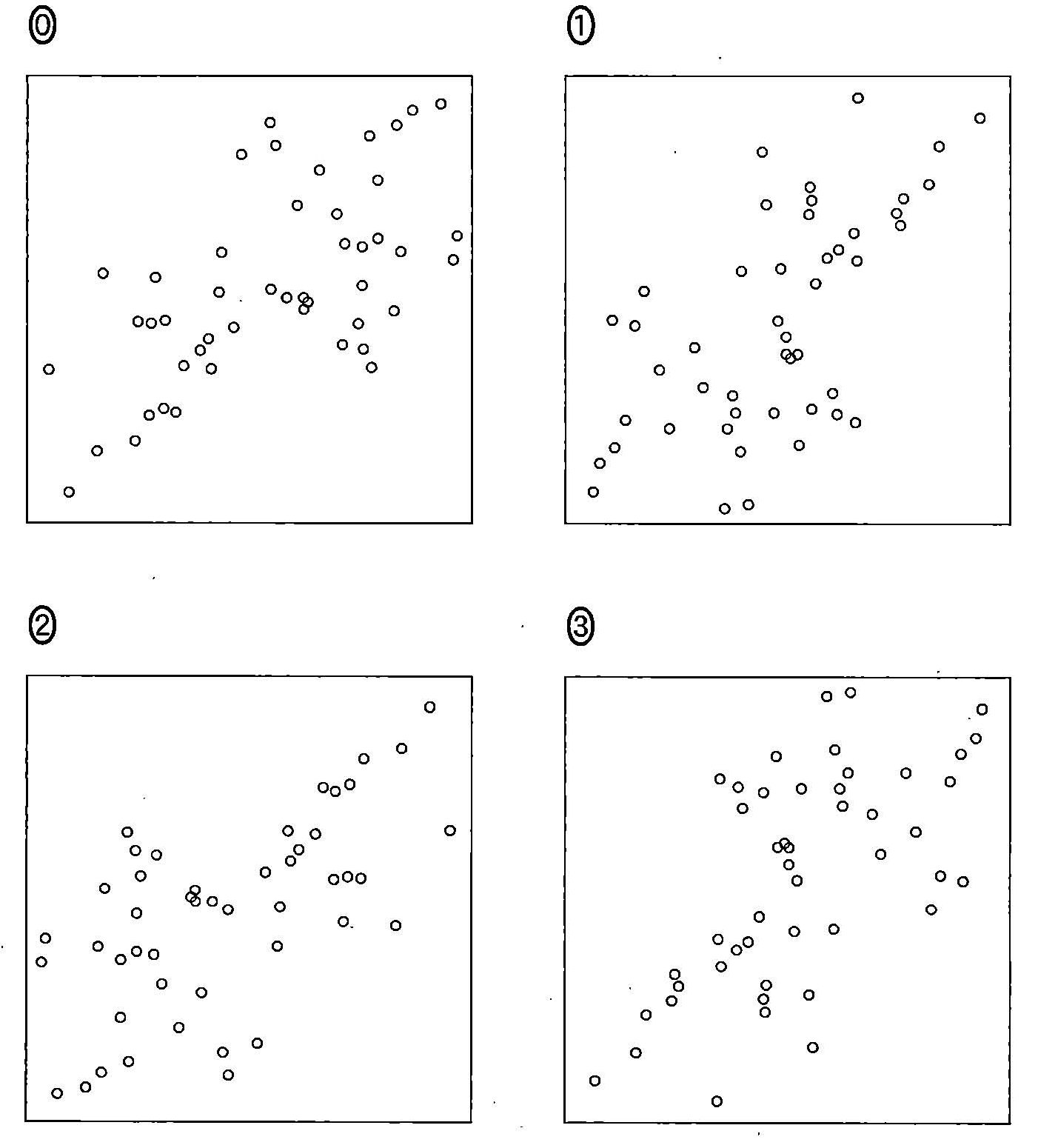
考慮到各行政區的總就業人數即為男性就業總數加上女性就業總數的前提， 2015 年度各行政區的總就業比例 (x 軸) 與女性就業比例 (y 軸) 的散佈圖理應為下列何者？ 請從下圖選出正確答案。此外圖省略了橫軸向右為正、縱軸向上為正的標記。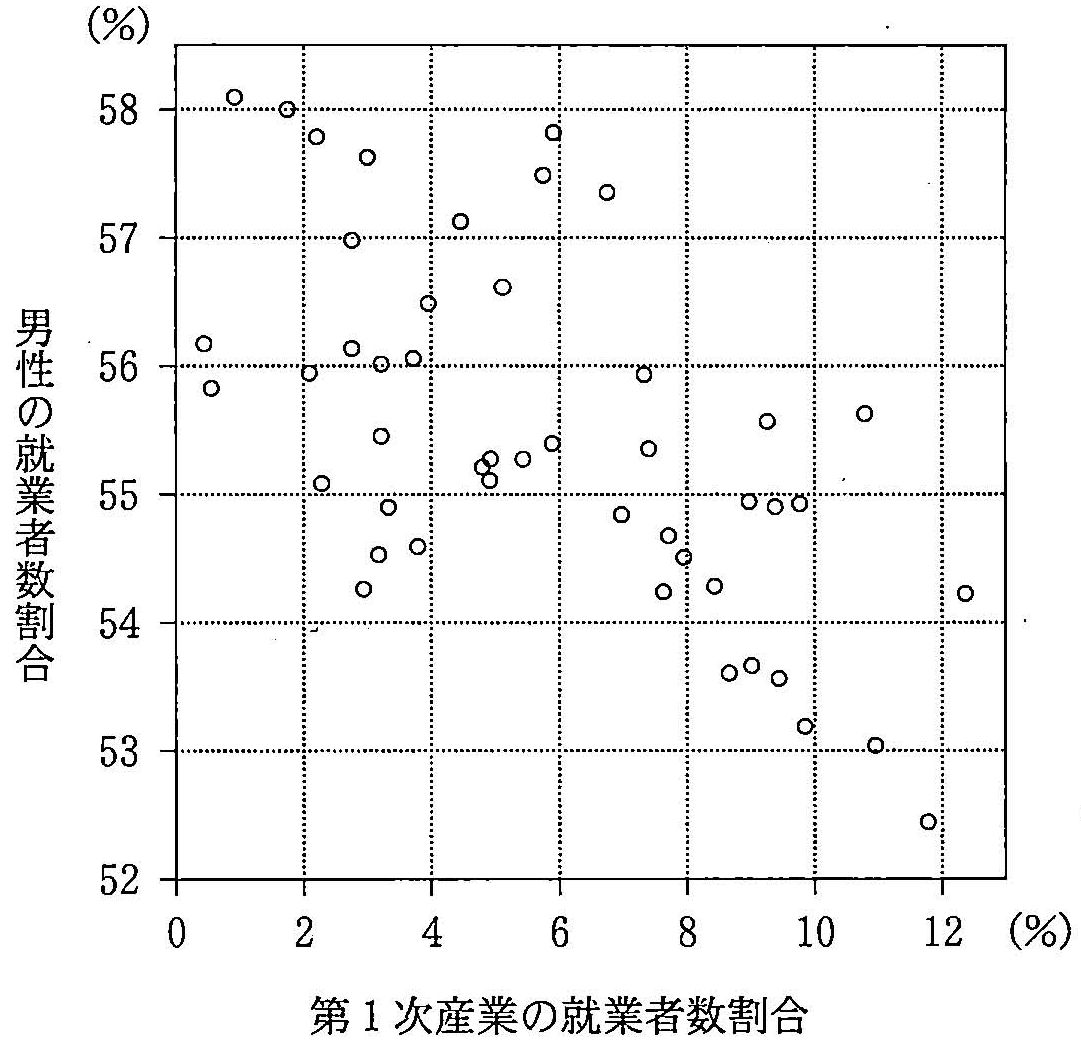
有多個外觀完全相同，但中獎機率不同的箱子。 請透過條件機率的觀點，從抽獎的結果推測是從哪個箱子抽出來的。(1) 假設有一個 1/2 中獎率的箱 A 與 1/3 中獎率的箱 B。(i) 針對每個箱子都抽三次。箱 A 抽三次正好中獎一次的機率為何...①？ 箱 B 抽三次正好中獎一次的機率為何...②？
(ii) 隨便選一個箱子。對該箱抽一個籤後再放回去，並重複三次，結果是正好中獎了一次。 此時，設事件 A 為「選中的是箱 A」、B 為「選中的是箱 B」， W 為「抽三次中一次」的現象，請解出下列機率。
因為機率是這樣 \(P(W)=P(A\cap W)+P(B\cap W)\)， 以三次中了一次為條件的 \(P(A|W)\) 結果為何？同時 \(P(B|W)\) 應該為何？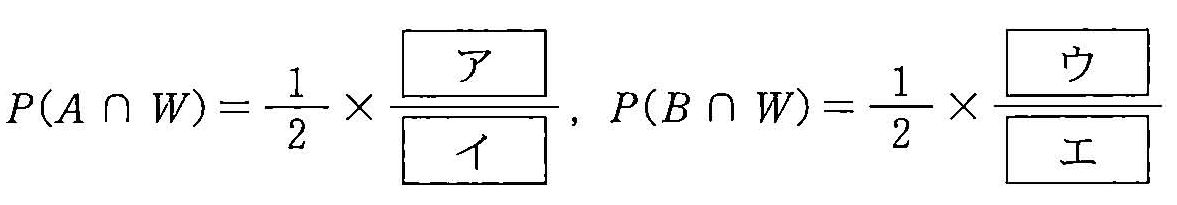
(2) 關於第 (1) 小題中的條件機率 \(P(A|W)\) 與 \(P(B|W)\)， 以及機率 ① 和 ②，下述事實 [*] 成立： 機率 \(P(A|W)\) 與 \(P(B|W)\) 的 [B] 等同於機率 ① 和 ② 的 [B]。 (兩個空格都是 [B]，選項如下)
0. 和 1. 兩倍的和 2. 三倍的和 3. 比 4. 積(3) 花子與太郎在聊上述事實。接下來考慮中獎率分別為 1/2, 1/3, 1/4 的箱 A、箱 B 與箱 C。 首先，隨意抽選一個箱子，重複三次抽一個籤再放回去的動作後，其中有一次中獎。 此時，剛剛選的箱子是箱 A 的條件機率為何？花子：為什麼上述事實 [*] 會成立啊？
太郎：透過計算 \(P(A|W)\) 與 \(P(B|W)\) 的過程中必要的結果， ① 和 ② 的機率都要乘以 1/2 的關係喔。
花子：原來如此！那如果有三個長得一樣的箱子，就都要乘以 1/3， 因此上述事實成立啊。
(4) 花子和太郎繼續對話。
花子：看來在三個箱子的狀況下，條件機率的 [B] (第 (2) 小題的答案) 就是各個箱子分別抽三次正好中獎一次的機率的 [B]。接下來考慮中獎率分別為 1/2, 1/3, 1/4, 1/5 的箱 A、箱 B、箱 C與箱 D。 首先，隨意抽選一個箱子，重複三次抽一個籤再放回去的動作後，其中有一次中獎。 此時，用條件機率的觀點來看，是選中哪一個箱子的機率從高至低排序如下：太郎：對呀！因此只要利用那個事實，不用額外計算條件機率也能比較出機率大小呢。
圓周上共有 15 個點，從 \(P_0\) 到 \(P_{14}\) 逆時鐘方向依序排開。 最初 \(P_0\) 上有一顆石頭。 接下來擲骰子決定，如果是偶數則將石頭逆時鐘移動 5 格， 如果是奇數則將石頭順時鐘移動 3 個點。 重複這個操作。 例如：石頭在 \(P_5\) 的時候，因為擲骰投出 6 而將石頭移動到 \(P_{10}\)， 下一次擲到 5 因此將石頭從 \(P_{10}\) 移動到 \(P_7\)。(1) 擲骰五次後，偶數共擲出□次、奇數共擲出□次的話，石頭會從 \(P_0\) 移動到 \(P_1\)。請使用二元一次方程式 \(5x-3y=1\) 求整數解以找出答案。(2) 令二元一次方程式 ② 為 \(5x-3y=8\)，所有可能的整數解表示如下（k 為整數）
在這之中，滿足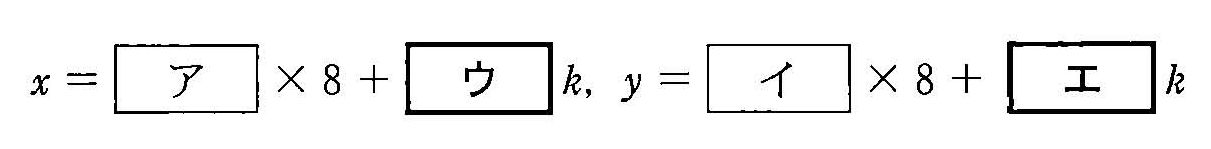
之條件的 x 為何？y 為何？（注意 y 的上界是前一個問題的答案。）
因此，骰子擲了 [C] 次以後，也就是擲出□次偶數、□次奇數（答案出現在前面了，不必重複作答），原本在 \(P_0\) 的石頭就會移動到 \(P_8\)。
(3) 承第 (2) 小題，有可能在總擲骰數少於 [C] 的狀況下， 讓石頭從 \(P_0\) 移動到 \(P_8\) 嗎？
【注意：石頭如果順時鐘移動 15 格、或者逆時鐘移動 15 格都會回到原點。】根據以上提示，擲出□次偶數、□次奇數，共計擲骰 [D] 次時， 石頭會從 \(P_0\) 移動到 \(P_8\)。此時 [D] < [C]。(4) 從 \(P_1\) 到 \(P_{14}\) 中隨意選一個點， 試圖讓在 \(P_0\) 的石頭依照上述規則移動到選定的點。 現在來討論為了達成這個目標，至少要擲骰幾次。 例如：只擲骰一次無法讓 \(P_0\) 的石頭移動到 \(P_1\)， 但擲兩次（一次偶數、一次奇數）後即可達成將 \(P_0\) 的石頭移動到 \(P_2\) 的目標。 因此，選擇 \(P_2\) 的時候，「最小擲骰次數」為 2 次。
\(P_1\) -- \(P_{14}\) 之中，需要最多「最小擲骰次數」的點為以下何者？ 共計需要□次。
0. \(P_{10}\) 1. \(P_{11}\) 2. \(P_{12}\) 3. \(P_{13}\) 4. \(P_{14}\)
ΔABC 各邊 AB=3, BC=4, AC=5。 \(\angle BAC\) 的角平分線與 BC 邊的交點命名為 D。試求此外，\(\angle BAC\) 的角平分線與 ΔABC 外接圓 O 的交點分別為 A 與 E。 關於 ΔAEC，試求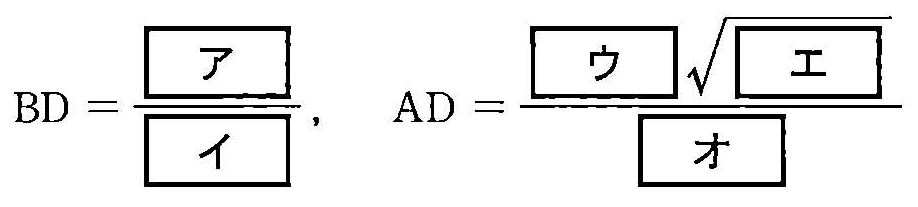
令圓 P（圓心在點 P）與 AB 和 AC 相切，且與圓 O 內切於點 F。 此外，圓 P 的半徑為 r，直線 PF 與外接圓 O 的交點為 F 與另一個點 G。此時
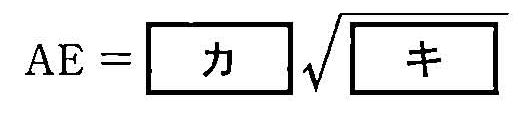因此，根據圓冪定理，\(\displaystyle r={\text{□}\over\text{□}}\)。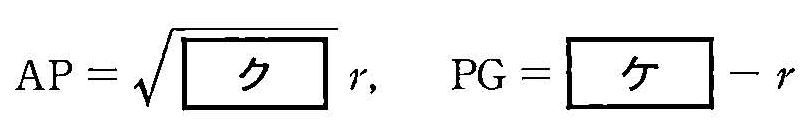
令 ΔABC 的內心為 Q，則內接圓 Q 的半徑為何？而 \(QA=\sqrt{\text{□}}\)？ 同時，圓 P 與 AB 邊的切點為 H，則 AH 為何？
承上，關於點 H 的描述 (a), (b) 的真偽如何？
- (a) 點 H 與 B, D, Q 在同一圓周上
- (b) 點 H 與 B, E, Q 在同一圓周上
