招聯會在 2022 年 11 月公布了民國 112 年大學招生的遊戲規則, 爆出「頂大理工科系不採記國文」的新聞, 引起部份學者憂心「頂尖大學不在乎人文素養」的言論。 中央大學中文系的朋友──胡川安教授──問:「只要國文成績好,就有人文素養〔嗎?〕」, 最後說:「採不採計國文科本來就和人文素養沒關」。 川安教授的意見,可以由測驗理論及國文考科的實徵資料支持。 本文想要從「工具理性」的觀點,回應川安教授。
在「不採計國文」之後不久,新聞又藉著李家同教授的貼文,喚起「新增 104 系不採記英文」的話題。 但這些不採記英文的學系並不來自「頂尖大學」,所以社會輿論大概認為是他們的招生策略,也就不多說什麼了。 其實,許多「頂尖大學」的文史哲領域學系採計數學,例如台大英文系在分發階段向來採計「數學乙」,某一年傳出不採計了,反而備受指責。 那些「要求」台大英文系採計數學乙的輿論,難道是因為在乎「數學素養」嗎? 我看倒也未必──他們是為了保留一個可以有效定「輸贏」的考科。
作者認為:大學招生時,採計/不採計一個考科的判準, 是它作為甄選學生的工具有效性,我們不必將它提升到「國民素養教育」的理想層次。
以下,我先解釋國文考科作為招生工具的相對「無效性」, 在過程中順便看到:數學 B 考科的工具效用很高, 因此呼籲人文社會領域值得採計數學 B。
根據作者在 2022 年 11 月 6 日從大考中心網站
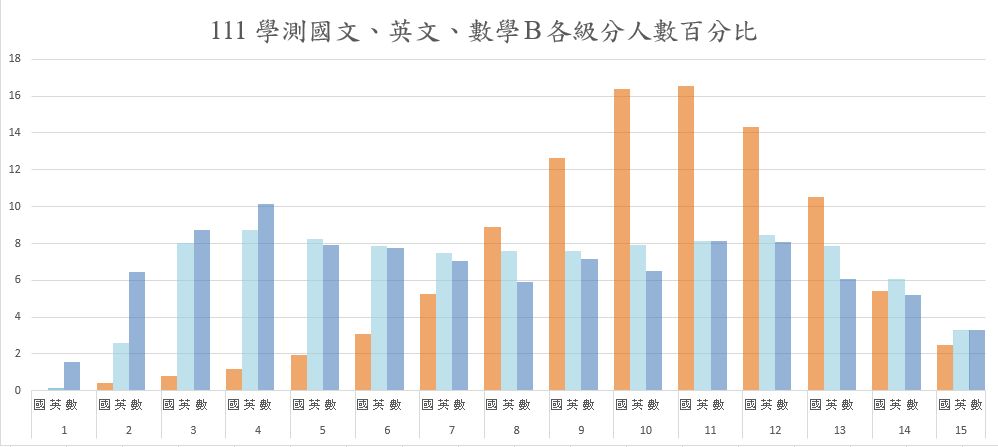
下載的數據,民國 111 年國文、英文、數學 B 這三個考科的 1-15 級分考生人數分布比率如下圖:
圖中明顯可見:國文科的分布如「鐘」,而英文、數學 B 則接近「均勻」。 這表示全國考生的國文科成績大多集中在 9、10、11、12、13 這些級分, 所以同分的人數很多──例如,將近二萬人同為 11 級分。 相對地,英文、數學 B 將考生相當「均勻」地分配在每個級分裡, 除了最高和最低級分以外,幾乎每個級分都框列了九千人。 在這個意義之下,我們說英文、數學 B 試卷的鑑別度高於國文試卷。
有些人以為一份考卷的成績應該是「正規分布」(鐘型分布)才「對」, 從以上英文、數學 B 考科的實徵資料來看,這個觀念是錯的。 根據數學理論,假如試卷中的每一題彼此獨立,而且每一題都有某個隨機做對的機率, 那麼一份試卷的總分,確實會呈現「鐘型」──也就是像上圖中的國文科分布。 可是,試卷中的題目不應該是彼此獨立的,而考生們盡力憑誠實作答,不都是隨機答題。 所以,試卷的成績分布,未必是鐘型。
事實上,以一份作為升學選才工具的測驗卷而言,最理想的表現是「均勻」分布, 也就是每個級分框列一樣多的考生。 根據上圖,111 年學測英文、數學 B 試卷的表現,就非常接近理想, 也證明理想中的試卷是可以被設計出來的。
更進一步檢視試卷,根據所謂的「古典測驗理論」, 試卷中的每一題(對當屆考生)都有「難度」和「鑑別度」兩個參數。 令難度坐標為橫軸、鑑別度坐標為縱軸, 則試卷中的每一題可以在坐標平面上畫出一個黑點:試卷有幾題,就畫幾個點。 這樣的圖簡稱「試題散佈圖」。
以下依序呈現 111 年學測國文、英文、數學 B 這三張試卷的試題散佈圖。 圖中每個黑點代表試卷內的一題,黑點越靠上表示鑑別度越高,越靠右表示那一題越簡單, 當然靠左就表示它難(答對率低)。
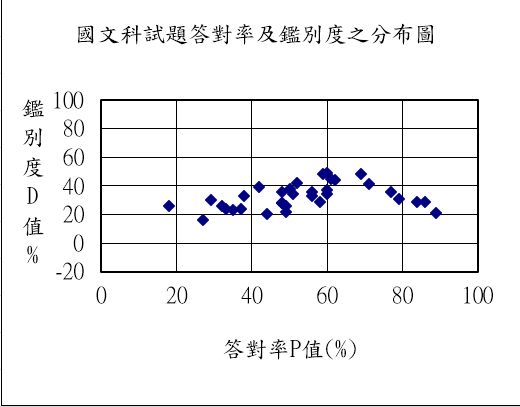
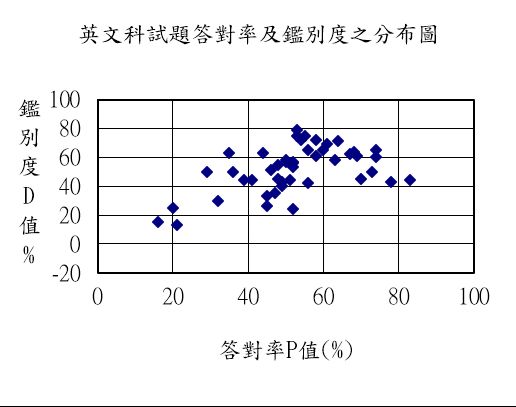
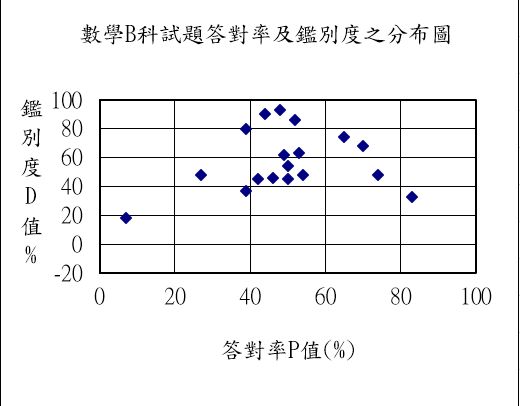
觀察上圖,相較之下,國文科沒有一題的鑑別度超過 0.60, 而英文科、數學 B 都有較高鑑別度的試題。 在英文、數學 B 的分布圖裡,我們看見較難和較易的題目,鑑別度都比較低, 這個現象符合「古典測驗理論」,算是正常的。 但是難度適中的題目則有機會創造較高的鑑別度, 我們從英文、數學 B 的散佈圖看到這個現象。 相對地,國文科的試題,不論難易,鑑別度差不多都一樣; 這表示每一題被「隨機」答對的成分有點重,於是也與前面看到的鐘型分布是一致的。
鐘型分布導致考科不容易區隔考生,而低鑑別度則表示這張試卷的成績不足以反應實際的學習成效。 後者,或許就是為什麼胡教授會說「只要國文成績好,就有人文素養(嗎?)」了。 寫這些意見,希望有助於國文科同仁設法改善國文試卷的命題與組卷技術。
以上資料,雖然僅為民國 111 年的學測成績, 但根據作者長年關心此事的觀察,國文、英文兩科, 在過去十年當中的鑑別力差不多都是如此,也就是國文科長期保持低鑑別力。 至於數學 B,因為它只考過一次,所以還沒有歷史資料。
數學 B 這一門課,確實是為了人文社會領域專業人士的「數學素養」而設計的。 但是前面說過了,遇到考試,我們暫且不高談「素養」的教育理想, 而專注於實際需求吧:那就是考科的工具效力。
數學 B 考科對前段、中段、後段的考生都能有效鑑別。在此工具裡性的意義下,「數學 B」非常適合用來當作招生工具。 更何況,如果能順便為「國民素養教育」盡一份心力,何樂而不為呢?