黃金比是個膾炙人口的數學常數,它有許多傳奇 — 或許太多了 — 以致於我的〈看郵票說數學的大歷史〉通識教材完全沒有提到它。但我最近需要幫忙一件事,需要從眾說一下黃金比。
黃金比 (golden ratio) — 通常記作 \(\Phi\) 或 \(\varphi\) — 是所謂黃金矩形 (golden rectangle) 的兩邊比,更確切地說是
的比值。而所謂黃金矩形是一種特殊長方形,當它被一條直線割出一塊正方形之後,剩下的部份與原來的長方形相似:也就是母子兩個矩形的邊長成比例。

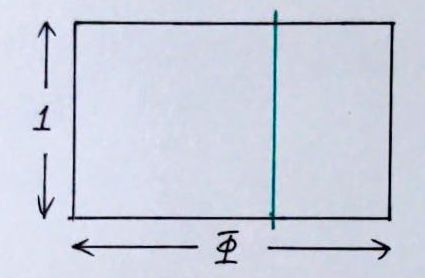
參閱上圖,它是一個黃金矩形的圖示。取大矩形的短邊為單位,則其短邊長為 \(1\),長邊長就是 \(\Phi\);割出一塊正方形之後,剩下的小矩形長邊為 \(1\) 而短邊為 \(\Phi-1\)。所以黃金比滿足 \[\Phi:1=1:(\Phi-1)\] 也就是說黃金比 \(\Phi\) 是比例式 \(x:1=1:(x-1)\) 的一個解,也就是二次方程 \[x^2-x=1\] 的解(另一個解為負數,不合)。所以 \[\Phi={1+\sqrt5\over2}\approx1.618\]
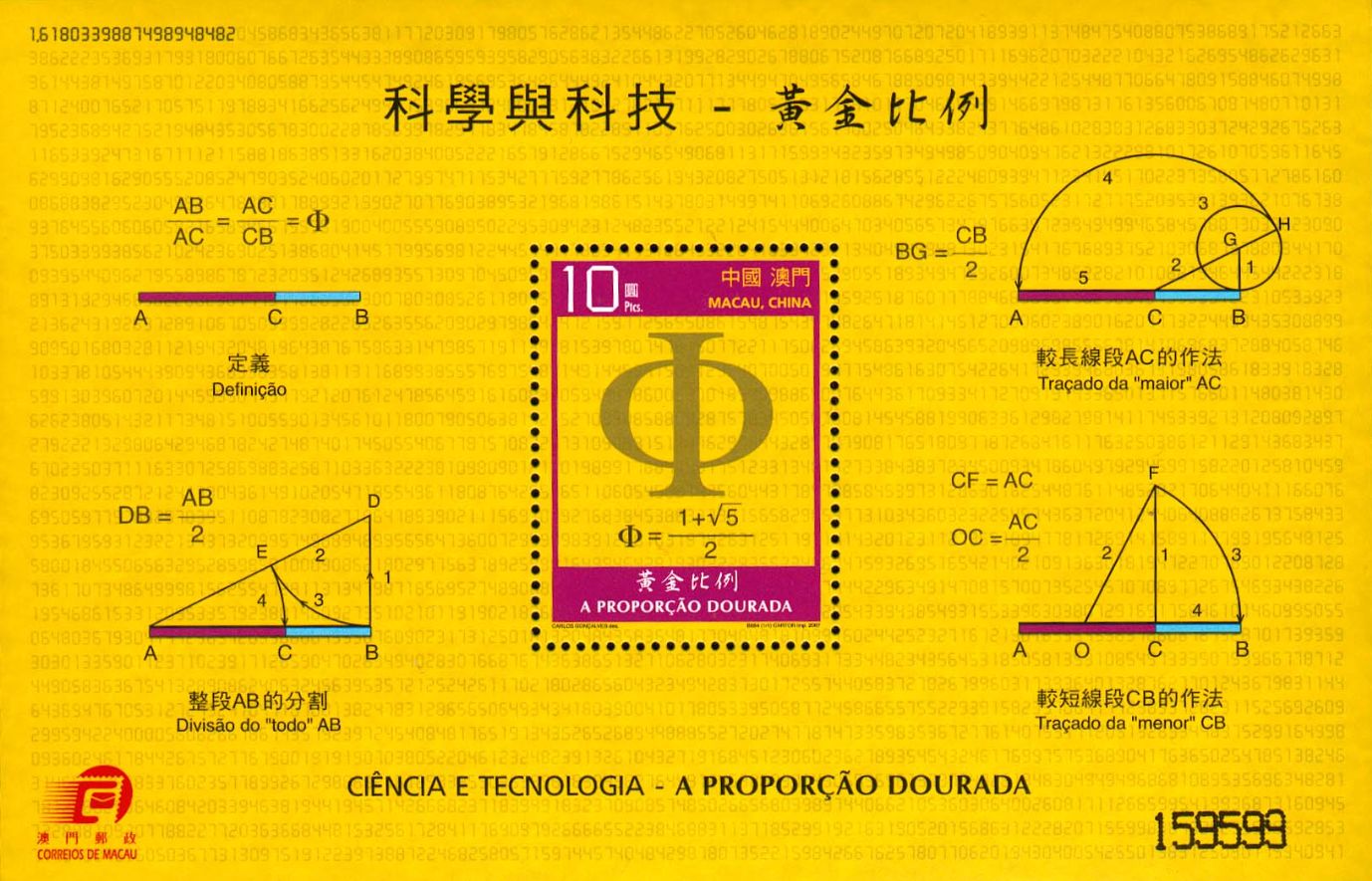
澳門在 2007 年發行五款黃金比郵票,併在兩張珍藏版上。版面上的外文是葡萄牙文,澳門曾是葡萄牙的殖民地。
第一張珍藏版上只有一枚 10 圓郵票,票面呈獻黃金比符號以及數值,外側四幅圖簡示的意義如下。
第二張珍藏版有八枚郵票,每一款各兩枚,背景是鸚鵡螺。

這四款郵票的畫面都是眾人傳頌的黃金比傳奇,幾乎都被收錄在中學課本裡,也很容易查到,簡述於下(上排左起)。
前面兩度提及費波納契數列 (Fibonacci sequence)。不是介紹黃金比嗎,提費波納契做什麼?這是一則中學課本裡的標準數學科普常識,也是以下這套郵票的主題。
列支敦斯登 (Liechtenstein) 是夾在奧地利與瑞士之間山地的小國,她的官方語言是德語,這個小「侯國」的面積只有 160 平方公里,大約是新竹市加上竹北的面積。此國郵政在 2013 年發行三枚套票,主題是從費波納契數列導引至黃金比。
所謂費波納契數列是
它的規則是從 1、1 這兩個數開始,此後每個數是前兩個數相加。我們看到前面說過的向日葵螺線的兩個數:21 和 34。
這套黃金比郵票的第一款如下,票面第一列文字寫著列支敦斯登的德文全名,兩個字之間插入黃金比符號 \(\Phi\)。第二列、第三列就是費波納契數列,省略第一個 1,以黑灰相間的數字呈現。但是注意最後的 100 並非數列,而是票面價值。所以最後一個黑色數字 676 也不完全,那個數應該是它前面兩個數相加,讀者可以自己算出來。

第二款顯示費波納契數列相鄰兩項的比值。黑灰相間,依序是 \[2\div1\quad3\div2\quad5\div3\quad8\div5\quad{13}\div8\quad {21}\div{13}\quad{34}\div{21}\quad\cdots\] 郵票上顯示的是「比」符號,但在德文算式中,「:」跟「÷」是同樣的意思。

這一系列的比值就是費波納契數列與黃金比的連結:這些比值將會「越來越靠近」黃金比。確切來說,這一系列的比值將會一上一下「包夾」黃金比 \(\Phi=1.618\cdots\),如下:
\(2\div1=2.000\cdots\)
\(3\div2=1.500\cdots\)
\(5\div3=1.666\cdots\)
\(8\div5=1.600\cdots\)
\({13}\div8=1.625\cdots\)
\({21}\div{13}=1.615\cdots\)
\({34}\div{21}=1.619\cdots\)
\(\cdots\)
第三款郵票就列印了黃金比的數值。對照前面澳門的黃金比全幅郵票,讀者有沒有發現兩者數值不太一樣?應該是列支敦斯登印錯了。

這套郵票本身的形狀就是黃金矩形。每一款郵票都放了一片樹葉,葉片的主要莖脈都安置在分割線上:也就是葉片的主脈大約形成一條鉛直線,直線的左邊割出正方形,右邊剩下一個較小的黃金矩形。葉片左側放了一幅淡色的黃金圓模版,可以用來協助平面圖案設計。模版有以下幾項規畫特色: