


Next: 積分
Up: 初等函數及其導函數
Previous: 三角函數
指數函數是指 ax, 式中 a 為實數.
同學們大概能說出 x 為正負整數或以奇數為分母的既約分數時 ax 的意義,
若 x 為以偶數為分母的既約分數, 則 ax 只當 a>0 時為實數.
因為在本課程中只談實數, 不談虛數, 所以以下我們假定 a>0.
但若 x 為無理數, 我們還沒給 ax 下過定義,
為此我們須使用上文索引入的連續函數的觀念.
由前面的極限定理可知; 設 f(x) 在 a 連續,  ,
,
 為常數, 則
為常數, 則
- (1)
-
 在 a 連續.
在 a 連續.
- (2)
- f(x)g(x) 在 a 連續.
- (3)
- 再設
 ,
則 f(x)/g(x) 在 a 連續.
,
則 f(x)/g(x) 在 a 連續.
由例 1 和例 3 知多項式及都是連續函數. 利用上面性質 (3),
可知有理函數在有定義的地方也都連續.
另外, 若 f'(a) 存在, 則 f 在 a 連續.
所以, 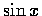 ,
,
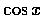 等許多三角函數都是連續函數.
(請參考本章末的習題 11).
等許多三角函數都是連續函數.
(請參考本章末的習題 11).
在下篇中, 我們將證明當 a>0 時有一個定義在整條實數軸上的連續函數 f(x),
使當 x 為有理數時有 f(x)=ax.
對 x 的無理數值, 我們仍用 ax 代表 f(x),
而稱之為指數函數 (exponential functions).
換言之, 我們可以連續地把 ax 的定義域從有理數延拓到整條實數軸.
在高中課本裡引進了一個怪數
稱之為自然對數的底.
這極限的存在一點也不明顯, 而在教育部的高中課程標準中又明令禁止證明它的存在.
在本教材的下冊中我們將對 e 詳加討論, 函數 ex 也可以寫作  ,
而稱之為自然 (natural) 指數函數.
,
而稱之為自然 (natural) 指數函數.
若 x=ay, 我們稱 y 為 x 以 a 為底的對數 (logarithm), 寫作
以 e, 10 和 2 為底的對數都非常重要, 因此都以特別的符號來表示,
 叫做自然對數 (natural logarithm),
可以表作
叫做自然對數 (natural logarithm),
可以表作  或
或  .
但
.
但  也常常用來表示常用對數 (common logarithm)
也常常用來表示常用對數 (common logarithm)
 .
.
 是組合學和計算機科學上常見的函數, 現在很多人用
是組合學和計算機科學上常見的函數, 現在很多人用
 表示它.
表示它.
自然對數函數和自然指數函數的微分公式是
利用公式
可得
又當 x>0 時, 從公式
 可得
可得
習

題
- 1.
- 證明
 .
.
- 2.
- 證明對任何實數 x 均有
 .
.
- 3.
- 證明
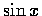 和
和 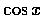 都是連續函數.
都是連續函數.
- 4.
- Sketch the graphs of the following functions,
with a discussion of their monotonicity
(where are they increasing or decreasing?) and concavity
(where are they concave upward or downward?),
and locate their extrema and points of inflection, if any:
(a)
x3-2x2-x=9, (b)
 ,
(c)
,
(c)
 .
.



Next: 積分
Up: 初等函數及其導函數
Previous: 三角函數
1999-06-27
![]() ,
,
![]() 為常數, 則
為常數, 則
 .
.
 ,
(c)
,
(c)
 .
.