


Next: 反三角函數
Up: 高中單變數微積分的補充
Previous: Hyperbolic Functions
設 f 為從集合 A 到集合 B 的映射.
若 x, 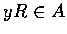 ,
且當 f(x)=f(y) 時必有 x=y,
則稱 f 為 one-one 映射.
若對任意的
,
且當 f(x)=f(y) 時必有 x=y,
則稱 f 為 one-one 映射.
若對任意的 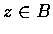 ,
均有
,
均有 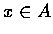 使 f(x)=z, 則稱 f 為 onto 映射.
既 one-one 又 onto 的映射, 叫做一一對應.
設 A, B 為數的集合, f 為從集合 A 到集合 B 的一一對應. 則對任意的
使 f(x)=z, 則稱 f 為 onto 映射.
既 one-one 又 onto 的映射, 叫做一一對應.
設 A, B 為數的集合, f 為從集合 A 到集合 B 的一一對應. 則對任意的 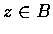 ,
均有唯一的
,
均有唯一的 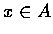 存在, 使 f(x)=z. 這方法對每一個 z 找到 x 和它對應,
遂定義了一個新的映射 x=g(z). 映射 g 叫作 f 的反映射;
它的定義域 (domain) 和值域 (range)
分別是原映射 f 的值域和定義域.
映射 f 的 反映射 g 常以 g=f-1 表示.
值域為數的集合的映射通稱函數.
我們習慣上用 x 代表函數的自變數. 在談 f(x)時, x 在 A 中變易,
而在談 g(x) 時, x 在 B 中變易.
反函數的例子極多. 如 x-3 便是 x+3 的反函數. 在高三的課中,
雖然沒有具體引入過反函數的名詞, 但讀者若細察對數函數的定義,
可知它便是指數函數的反函數. 一般地講, 一個狹義增或減的函數必有反函數.
若一函數沒有反函數, 我們可以縮小它的定義域, 使它有反函數.
令 D 表函數 f 的定義域, 即若
存在, 使 f(x)=z. 這方法對每一個 z 找到 x 和它對應,
遂定義了一個新的映射 x=g(z). 映射 g 叫作 f 的反映射;
它的定義域 (domain) 和值域 (range)
分別是原映射 f 的值域和定義域.
映射 f 的 反映射 g 常以 g=f-1 表示.
值域為數的集合的映射通稱函數.
我們習慣上用 x 代表函數的自變數. 在談 f(x)時, x 在 A 中變易,
而在談 g(x) 時, x 在 B 中變易.
反函數的例子極多. 如 x-3 便是 x+3 的反函數. 在高三的課中,
雖然沒有具體引入過反函數的名詞, 但讀者若細察對數函數的定義,
可知它便是指數函數的反函數. 一般地講, 一個狹義增或減的函數必有反函數.
若一函數沒有反函數, 我們可以縮小它的定義域, 使它有反函數.
令 D 表函數 f 的定義域, 即若
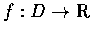 ,
,
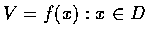 稱為 f 的像 (image).
當我們縮小定義域至 D 的子集合 D' 以定義反函數時,
通常不能把 D' 選得太大, 才能使得 f 在 D' 上為一一函數,
但也不願把它選得太小, 因為我們也希望維持函數的像 V 不變.
稱為 f 的像 (image).
當我們縮小定義域至 D 的子集合 D' 以定義反函數時,
通常不能把 D' 選得太大, 才能使得 f 在 D' 上為一一函數,
但也不願把它選得太小, 因為我們也希望維持函數的像 V 不變.
例如 f(x)=x2 沒有反函數, 它的像是 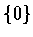 和正實數所形成的集合.
如果我們把它的定義域也縮小為
和正實數所形成的集合.
如果我們把它的定義域也縮小為 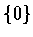 和正實數, 那麼反函數就存在了:
它便是
和正實數, 那麼反函數就存在了:
它便是
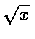 .
但這種縮小定義的方法並不是唯一的;
我們也可以把它縮小為
.
但這種縮小定義的方法並不是唯一的;
我們也可以把它縮小為 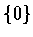 和所有負實數,
這時反函數是
和所有負實數,
這時反函數是
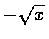 ,
或縮小為
,
或縮小為
![$[-1,0]\cup(1,\infty)$](img30.gif) ,
這時反函數當
,
這時反函數當 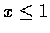 時是
時是 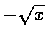 ,
當 x>1 時
,
當 x>1 時 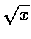 .
在描繪函數的圖形時, 我們也習慣以 x 軸表自變數, 以 y 軸表函數.
當我們在一張透明的紙上繪出一個函數的圖形,
將該紙沿直線 y=x 旋轉
.
在描繪函數的圖形時, 我們也習慣以 x 軸表自變數, 以 y 軸表函數.
當我們在一張透明的紙上繪出一個函數的圖形,
將該紙沿直線 y=x 旋轉
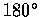 ,
於是紙的背面變成了紙的正面,
x 軸和 y 軸的位置互換了, 而原函數的圖形也就變成了它的反函數的圖形.
設 f 為區間 (a,b) 中的連續狹義單調函數.
我們假定 f' 在 (a,b) 中存在, 且到處
,
於是紙的背面變成了紙的正面,
x 軸和 y 軸的位置互換了, 而原函數的圖形也就變成了它的反函數的圖形.
設 f 為區間 (a,b) 中的連續狹義單調函數.
我們假定 f' 在 (a,b) 中存在, 且到處 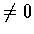 .
令 g 為 f 的反函數. 如果我們假定 g'(x) 存在,
則其值可依下法計算之:
從反函數的定義知 f(g(x))=x. 利用連鎖律將兩邊微分得
.
令 g 為 f 的反函數. 如果我們假定 g'(x) 存在,
則其值可依下法計算之:
從反函數的定義知 f(g(x))=x. 利用連鎖律將兩邊微分得
因此有
這就是反函數的微分公式. 若 y=g(x), 則 x=f(y).
上公式可記作
這是能幫助記憶的寫法, 但是使用時必須把它的意義弄清楚, 才不致出問題.
這公式的幾何意義非常明顯: 當我們將一個函數的圖形沿直線
y=x 旋轉
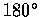 至紙的反面時,
它的切線的斜率便變成其倒數了.
假若原函數在
(x0,y0) 處有非水平的切線,
則經旋轉
至紙的反面時,
它的切線的斜率便變成其倒數了.
假若原函數在
(x0,y0) 處有非水平的切線,
則經旋轉
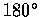 後變成反函數在
(y0,x0) 處有非鉛直的切線.
後變成反函數在
(y0,x0) 處有非鉛直的切線.
習

題
- 1.
- 設 a, b 為實數, 且
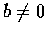 ,
試證
,
試證
- 2.
- 試導出
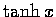 的加法公式.
的加法公式.
- 3.
- 試求
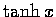 ,
,
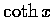 ,
,
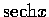 和
和
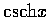 的導函數.
的導函數.
- 4.
- 令
f(x)=x4+4x-1.
(a) 求 f 的定義域 D 與像 V.
(b) 試描繪出 f 的圖形.
(c) 取 D 的子集合 D', 使 f 在 D' 上為一一函數, 且其像不變.
- 5.
- 令
f(x)=(x+1)(x2+3x-4).
(a) 求 f 的定義域 D 與像 V.
(b) 試畫出 f 的圖形.
(c) 取 D 的子集合 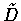 ,
使得 f 在
,
使得 f 在 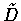 上為一一的,
且其像仍為 V.
上為一一的,
且其像仍為 V.
- 6.
- 設 f(x) 為 (a,b) 中的可微增函數,
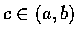 ,
f(c)=d, f'(c)=0, g=f-1. 試證 g 在 d 處必不可微.
,
f(c)=d, f'(c)=0, g=f-1. 試證 g 在 d 處必不可微.



Next: 反三角函數
Up: 高中單變數微積分的補充
Previous: Hyperbolic Functions
1999-06-27
![]() 和正實數所形成的集合.
如果我們把它的定義域也縮小為
和正實數所形成的集合.
如果我們把它的定義域也縮小為 ![]() 和正實數, 那麼反函數就存在了:
它便是
和正實數, 那麼反函數就存在了:
它便是
![]() .
但這種縮小定義的方法並不是唯一的;
我們也可以把它縮小為
.
但這種縮小定義的方法並不是唯一的;
我們也可以把它縮小為 ![]() 和所有負實數,
這時反函數是
和所有負實數,
這時反函數是
![]() ,
或縮小為
,
或縮小為
![]() ,
這時反函數當
,
這時反函數當 ![]() 時是
時是 ![]() ,
當 x>1 時
,
當 x>1 時 ![]() .
在描繪函數的圖形時, 我們也習慣以 x 軸表自變數, 以 y 軸表函數.
當我們在一張透明的紙上繪出一個函數的圖形,
將該紙沿直線 y=x 旋轉
.
在描繪函數的圖形時, 我們也習慣以 x 軸表自變數, 以 y 軸表函數.
當我們在一張透明的紙上繪出一個函數的圖形,
將該紙沿直線 y=x 旋轉
![]() ,
於是紙的背面變成了紙的正面,
x 軸和 y 軸的位置互換了, 而原函數的圖形也就變成了它的反函數的圖形.
設 f 為區間 (a,b) 中的連續狹義單調函數.
我們假定 f' 在 (a,b) 中存在, 且到處
,
於是紙的背面變成了紙的正面,
x 軸和 y 軸的位置互換了, 而原函數的圖形也就變成了它的反函數的圖形.
設 f 為區間 (a,b) 中的連續狹義單調函數.
我們假定 f' 在 (a,b) 中存在, 且到處 ![]() .
令 g 為 f 的反函數. 如果我們假定 g'(x) 存在,
則其值可依下法計算之:
從反函數的定義知 f(g(x))=x. 利用連鎖律將兩邊微分得
.
令 g 為 f 的反函數. 如果我們假定 g'(x) 存在,
則其值可依下法計算之:
從反函數的定義知 f(g(x))=x. 利用連鎖律將兩邊微分得
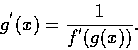
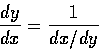
![]() 至紙的反面時,
它的切線的斜率便變成其倒數了.
假若原函數在
(x0,y0) 處有非水平的切線,
則經旋轉
至紙的反面時,
它的切線的斜率便變成其倒數了.
假若原函數在
(x0,y0) 處有非水平的切線,
則經旋轉
![]() 後變成反函數在
(y0,x0) 處有非鉛直的切線.
後變成反函數在
(y0,x0) 處有非鉛直的切線.