


Next: 弧長
Up: 微積分的幾何應用
Previous: 向量值函數與曲線
除了利用直角座標系表示平面上的點外,
還有另一種利用一對實數表示平面上的一點的方法. 設 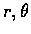 為二實數. 令
為二實數. 令
再令 P 為直角座標為(x,y)的點,
則
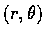 稱為 P 點的一組極座標 (polar coordinates);
r 叫 P 的向徑 (radius vector),
稱為 P 點的一組極座標 (polar coordinates);
r 叫 P 的向徑 (radius vector),
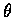 叫 P 的 輻角 (amplitude).
叫 P 的 輻角 (amplitude).
給定 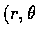 ), 則以 (
), 則以 (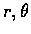 )
為極座標的點 P 便完全確定了.
但反之, 若給定了點 P, 其極座標 (
)
為極座標的點 P 便完全確定了.
但反之, 若給定了點 P, 其極座標 (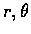 )
卻不能完全確定.
若 P 為原點, 則對任意
)
卻不能完全確定.
若 P 為原點, 則對任意
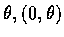 都是它的極座標.
若 P 不是原點, (
都是它的極座標.
若 P 不是原點, (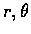 )是它的一組極座標,
則 P 的所有極座標的集合為
)是它的一組極座標,
則 P 的所有極座標的集合為
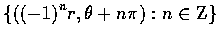 ,
式中
,
式中
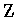 表示所有整數的集合.
但另一方面, 任意點 P 都至少有一組(因而便有無限多組)極座標. 事實上,
設 (x,y) 為 P 的直角座標.
若 x=y=0, 則無論
表示所有整數的集合.
但另一方面, 任意點 P 都至少有一組(因而便有無限多組)極座標. 事實上,
設 (x,y) 為 P 的直角座標.
若 x=y=0, 則無論 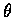 怎麼取,(
怎麼取,(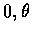 )都是 P 的極座標.
當 x,y 不同時為0時, 令
)都是 P 的極座標.
當 x,y 不同時為0時, 令
時, 則 (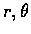 )為 P 的一組極座標.
高中課本中雖然沒討論過極座標, 但曾引進過複數的觀念.
其實我們可以把二維空間中的點看作複數, 這點的兩個座標便是複數的實部和虛部.
換言之, 對應於
)為 P 的一組極座標.
高中課本中雖然沒討論過極座標, 但曾引進過複數的觀念.
其實我們可以把二維空間中的點看作複數, 這點的兩個座標便是複數的實部和虛部.
換言之, 對應於
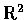 中的點 P=(x,y) 令 z(P)=x+yi(式中
中的點 P=(x,y) 令 z(P)=x+yi(式中
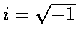 ). 則 z 是從
). 則 z 是從
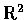 到所有複數集的一一對應.
令 r=|z(P)|, 則
到所有複數集的一一對應.
令 r=|z(P)|, 則 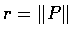 .
又令
.
又令
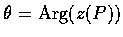 .
則 (
.
則 (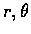 )
便是點 P 的一組極座標.
點的極座標 r 和
)
便是點 P 的一組極座標.
點的極座標 r 和 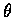 間可能滿足某種關係式.
如果所有滿足該關係式的點形成一曲線,
則該關係式叫作曲線的 極方程式 (polar eqution).
例如若
間可能滿足某種關係式.
如果所有滿足該關係式的點形成一曲線,
則該關係式叫作曲線的 極方程式 (polar eqution).
例如若 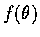 為
為 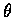 的連續函數,
令 C 表示極方程式
的連續函數,
令 C 表示極方程式
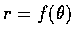 所定義的曲線,
則可視
所定義的曲線,
則可視 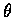 為參數, 立刻得到 C 在直角座標系下的參數方程式:
為參數, 立刻得到 C 在直角座標系下的參數方程式:
利用極方程式繪圖最好用極座標紙. 這種紙上印有呈蜘蛛網形狀的圖形.
圖形的中心是圓點, 圍繞著圓點有很多同心圓, 表示 r =常數;
通過原點又有很多射線, 表示 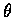 =常數.
你如果買不到這種紙, 建議你自己繪製一張, 然後利用影印機複製一些,
因為有很多有趣的曲線都是用極方程式表示的. 茲舉例如下:
=常數.
你如果買不到這種紙, 建議你自己繪製一張, 然後利用影印機複製一些,
因為有很多有趣的曲線都是用極方程式表示的. 茲舉例如下:
現在我們想將極座標的觀念推廣到三維空間. 推廣的方法有二:
我們用 (x,y,z) 表示三維空間中一點 P 的直角座標系.
如果在 xy 平面中引入極座標系
則點 P 可由
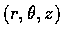 完全決定.
完全決定.
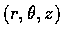 叫作 P 的圓柱座標 (cylindrical coordinates).
叫作 P 的圓柱座標 (cylindrical coordinates).
設座標系的原點為 O 連接 OP , 令 OQ 為 OP 在 xy 平面上的投影.
設自正 x 軸旋轉至射線 OQ 的角為 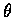 ,
自射線 OQ 旋轉至射線 OP 的角為
,
自射線 OQ 旋轉至射線 OP 的角為 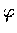 .
再令 OP 的長為
.
再令 OP 的長為 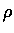 .
則
.
則
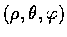 叫作點 P 的球座標 (spherical coordinates).
球座標和直角座標的關係如下:
叫作點 P 的球座標 (spherical coordinates).
球座標和直角座標的關係如下:
通常我們選擇
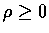 ,
,
![$\theta\in{[0,2\pi]}$](img161.gif) ,
,
![$\varphi\in [-\pi/2,\pi/2]$](img162.gif) .
.
習

題
- 1.
- Find a formula to compute the distance between the points in the plane
whose polar coordinates are
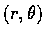 and
and
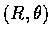 .
Also find a similar formula for spherical coordinates in
.
Also find a similar formula for spherical coordinates in
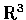 .
.
- 2.
- 試證自橢圓上任一點至兩焦點的連線, 與該點處切線之交角相等.
- 3.
- (a) 試求 cycloid 上任一點處切線的方程式.
(b) 試求 helix 上任一點處切線的方程式.
- 4.
- The curve whose polar equation is
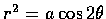 ,
where a>0, is called a lemniscate (雙紐線).
Sketch its graph, and find the area inside one of its two loops.
,
where a>0, is called a lemniscate (雙紐線).
Sketch its graph, and find the area inside one of its two loops.
- 5.
- 以
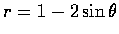 為極方程式的曲線叫做 limacon.
試繪出它的圖形,
並求其內部小閉曲線所圍成的面積.
為極方程式的曲線叫做 limacon.
試繪出它的圖形,
並求其內部小閉曲線所圍成的面積.
- 6.
- 在三維空間中考慮向量值函數
試證 (1,2,0) 為該曲線和本身的交點, 並求出該交點處曲線的兩條切線.
- 7.
- 試寫出 four-leaved rose 及 five-leaved rose 之方程式, 並繪出其圖形.
- 8.
- 將一條纏繞在一固定圓形線軸的絲線拉直繞開. 試求此線端點軌跡的極方程式,
並繪出此曲線.
註. 這曲線叫做 involute of the circle.
- 9.
- 極方程式為
的曲線當 0<e<1 時為橢圓, e=1 時為拋物線, e>1 時為雙曲線. 試證明之.
- 10.
- Find the area of the common interior of the cardioid
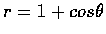 and the circle
and the circle
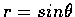 .
.
- 11.
- 設
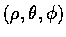 為空間一點 P 的一組球座標.
試寫出 P 的所有球座標的集合.
為空間一點 P 的一組球座標.
試寫出 P 的所有球座標的集合.



Next: 弧長
Up: 微積分的幾何應用
Previous: 向量值函數與曲線
1999-06-27
![]() ), 則以 (
), 則以 (![]() )
為極座標的點 P 便完全確定了.
但反之, 若給定了點 P, 其極座標 (
)
為極座標的點 P 便完全確定了.
但反之, 若給定了點 P, 其極座標 (![]() )
卻不能完全確定.
若 P 為原點, 則對任意
)
卻不能完全確定.
若 P 為原點, 則對任意
![]() 都是它的極座標.
若 P 不是原點, (
都是它的極座標.
若 P 不是原點, (![]() )是它的一組極座標,
則 P 的所有極座標的集合為
)是它的一組極座標,
則 P 的所有極座標的集合為
![]() ,
式中
,
式中
![]() 表示所有整數的集合.
但另一方面, 任意點 P 都至少有一組(因而便有無限多組)極座標. 事實上,
設 (x,y) 為 P 的直角座標.
若 x=y=0, 則無論
表示所有整數的集合.
但另一方面, 任意點 P 都至少有一組(因而便有無限多組)極座標. 事實上,
設 (x,y) 為 P 的直角座標.
若 x=y=0, 則無論 ![]() 怎麼取,(
怎麼取,(![]() )都是 P 的極座標.
當 x,y 不同時為0時, 令
)都是 P 的極座標.
當 x,y 不同時為0時, 令
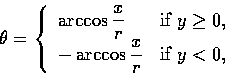
![]() ,
自射線 OQ 旋轉至射線 OP 的角為
,
自射線 OQ 旋轉至射線 OP 的角為 ![]() .
再令 OP 的長為
.
再令 OP 的長為 ![]() .
則
.
則
![]() 叫作點 P 的球座標 (spherical coordinates).
球座標和直角座標的關係如下:
叫作點 P 的球座標 (spherical coordinates).
球座標和直角座標的關係如下: