


Next: Limit and Continuity
Up: 多變數函數的微分學
Previous: 多變數函數的微分學
設 D 為
 內一區域, f 為從 D 到
內一區域, f 為從 D 到
 的對應,
則 f 為一
的對應,
則 f 為一
 值的 n 變數函數.
在本課程中將只討論實數值, 即 m=1 時的情形.
值的 n 變數函數.
在本課程中將只討論實數值, 即 m=1 時的情形.
設
 仿單變數情況,
我們稱
仿單變數情況,
我們稱
 為 f 的函數圖.
另一方面,
若
為 f 的函數圖.
另一方面,
若
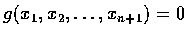 為 n+1 個未知數
為 n+1 個未知數
 的方程式, 則集合
的方程式, 則集合
稱為該方程式的圖形.
利用這個說法, 上述的函數圖也可以看成方程式
xn+1=f(x)
的圖形. 當 n=2 時, f 的函數圖在
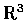 中可以實際圖示,
對 f 的瞭解幫助很大. 此外也可藉等位集 (level sets) 加以了解:
設 c 為實數, 則
中可以實際圖示,
對 f 的瞭解幫助很大. 此外也可藉等位集 (level sets) 加以了解:
設 c 為實數, 則
就叫做一個等位集. 這是 f 的值等於 c 的地方.
當 n=2 或 3 時 level sets 又分別稱為 levl curves
(等高線)或 level surfaces (等位面).
設 a, b 為二常數,
則函數
f(x, y)=ax+by+c 的圖形為和 z 軸相交的平面.
反之, 和 z 軸相交的平面也都可以以這樣的方程式表示.
和 z 軸平行的平面的方程式則成 ax+by+c=0 之形,
式中 a 和 b 不同時為 0.
以下我們舉兩個二次函數圖形的例子. 令
這函數的圖形叫做 elliptic paraboloid , 其等高線均為橢圓.
另一方面, 該曲面和平面 x=c 或 y=c 的交界均為拋物線, 故得其名.
函數
的圖形叫做hyperbolic paraboloid, 它的等高線均為雙曲線.
這個 hyperbolic paraboloid 頗有興趣: 它和 xz 平面的交界為一拋物線開口向上,
以原點為極小, 而它和 yz 平面的交界亦為一拋物線開口向下, 以原點為極大.
整個曲面成一馬鞍的形狀, 原點叫做它的鞍點 (saddle point).
新竹清華大學梅園中梅亭的建築, 便約略呈這個圖的形狀.
若
f(x, y, z) 為三變數 x, y, z 的二次式,
則滿足方程式
f(x, y, z)=0 的點的集合叫做一個二次曲面
(Quadric surface).
上面已經介紹的兩種 paraboloids . 都是二次曲面的例子.
以下我們順便討論一下別種三個變數的二次曲面. 高中課程中曾討論過二次曲面.
依方程式的不同, 二次曲面除退化情況以外有拋物線、橢圓、雙曲線三種.
二次曲面是二次曲線至三維空間的推廣. 類似於等高線,
在討論二次曲面時我們也觀察它們和三個座標面平行的平面上的截口
(intercepts).
在以下的討論中, 設 a,b,c 均為正數, 方程式呈
形的曲面叫 ellipsoid (橢球). 它在和三個坐標面平行的平面上的截口全都是橢圓.
當 a=b=c 時, ellipsoid叫做球 (sphere).
當  時, 它叫做 speroid.
視 a>c 或 a<c , 這 spheroid 呈鐵餅形或橄欖球形,
分別叫做 prolate 及 oblate spheroid.
時, 它叫做 speroid.
視 a>c 或 a<c , 這 spheroid 呈鐵餅形或橄欖球形,
分別叫做 prolate 及 oblate spheroid.
方程式呈
形的曲面叫 elliptic hyperboloid of one sheet.
它在和 xy 平面平行的平面上的截口亦均為橢圓, 離 xy 平面愈遠的愈大.
但它在和 xz 及 yz 平面平行的平面上的截口則皆為雙曲線.
所謂 elliptic hyperboloid of two sheets 是指方程式為
的圖形而言. 它在和 xy 及 xz 平面平行的平面上的截口則亦均為雙曲線,
離坐標平面愈遠的主軸愈大, 它在和 yz 平面平行的平面上或無截口,
或截口為橢圓.
最後介紹 elliptic cone: 這曲面的方程式是
當 a=b 時, 它叫做圓錐 (circular cone, 或簡稱 cone).
讓圓錐和不同的平面相交, 則交界可得各種的二次曲線.
因此二次曲線也叫做圓錐曲線 (conics).



Next: Limit and Continuity
Up: 多變數函數的微分學
Previous: 多變數函數的微分學
1999-06-28
![]() 仿單變數情況,
我們稱
仿單變數情況,
我們稱
![]() 為 f 的函數圖.
另一方面,
若
為 f 的函數圖.
另一方面,
若
![]() 為 n+1 個未知數
為 n+1 個未知數
![]() 的方程式, 則集合
的方程式, 則集合