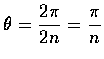 .
一個典型的三角形以
.
一個典型的三角形以
考慮一個圓柱面, 設其高為 h, 其底圓的半徑為 1. 我們將頂圓和底圓的周界分別分成 2n 等分. 分割時注意務使每個頂圓的分點落在對應的底圓分點的正上方. 將頂圓的每個奇數分點和底圓上和他最接近的兩個偶數分點相連接, 最後再將頂圓相鄰的奇數分點相連,將底圓相鄰的偶數分點相連, 如是乃得 2n 個等腰三角形. 以下我們要計算這些三角形的總面積 T.
因為所有的三角形皆全同, 所以我們只需計算其中任意一個三角形的面積 A.
令
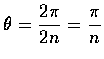 .
一個典型的三角形以
.
一個典型的三角形以
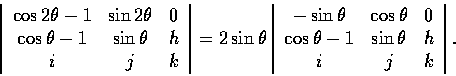
現在考慮以 1 為高也以 1 為底圓半徑的圓柱面.
因為我們可以把這圓柱面沿一條母線剪開,
攤在平面上, 得一以 ![]() 為底, 以 1 為高的矩形,
所以圓柱面的表面積應該是
為底, 以 1 為高的矩形,
所以圓柱面的表面積應該是 ![]() .
我們將此圓柱面用水平面分割成 m 個薄片,
使每片的高均為
.
我們將此圓柱面用水平面分割成 m 個薄片,
使每片的高均為
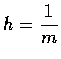 .
再依上法將每個薄片分成 2n 個三角形.
則 m 個薄片上共有 2mn 個三角形, 其總面積為
.
再依上法將每個薄片分成 2n 個三角形.
則 m 個薄片上共有 2mn 個三角形, 其總面積為
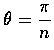 ,
故當
,
故當
1)設 m=n. 此時
![]() ,
所以有
,
所以有
![]() .
這正是我們所要的表面積的值.
.
這正是我們所要的表面積的值.
2)設 m=n2. 此時
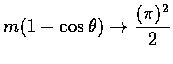 ,
所以有
,
所以有
3)設 m=n3. 此時可證
![]() .
讀者不妨自己作一作.
.
讀者不妨自己作一作.
以上的討論顯示在定義表面積時, 推廣定義弧長的方法竟歸於失敗. 所以我們不宜利用曲面的內接多面體的面積作其近似. 定義表面積須另闢蹊徑. 但在介紹正確的方法以前, 我們必須先解釋一下什麼是曲面.
仿造利用參數式定義曲線的法子, 可以定義曲面如次:
設 D 為 uv 平面上的區域,
![]() 為連續映像,
則稱 f 或它的像集合
為連續映像,
則稱 f 或它的像集合
在以下的討論中, 令
![]() ,
f 如上. 我們要定義曲線面
S: (x, y, z)=f(u, v) 的表面積.
,
f 如上. 我們要定義曲線面
S: (x, y, z)=f(u, v) 的表面積.
將 [a, b] 和 [c, d] 分割如下:
![]() ,
,
![]() .
對
.
對
![]() 定義
定義
The solution of the last problem suggests a more general situation:
Consider the curve z=f(x),
![]() in the xz-plane.
When this curve is revolved about the z-axis,
there results a surface of revolution whose equation in cylindrical coordinates is z=f(r),
in the xz-plane.
When this curve is revolved about the z-axis,
there results a surface of revolution whose equation in cylindrical coordinates is z=f(r),
![]() .
Then
.
Then
![\begin{displaymath}\int_0^{2\pi}d \theta \int_a^b \sqrt{1+[f'(r)]^2}rdr=2\pi \int_a^b \sqrt{1
+[f'(x)]^2}x\, dx.
\end{displaymath}](img28.gif)
讀者可以試用本公式再計算一次球的表面積. 以下我們用此公式來計算圓錐的表面積:
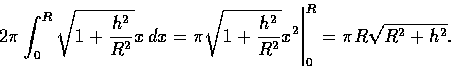
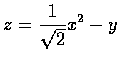 被四平面
被四平面
![\begin{displaymath}\displaystyle\int_\Omega\sqrt{r^2+[rf_r(r, \theta)]^2+[f_\theta(r, \theta)]^2}drd\theta.
\end{displaymath}](img39.gif)