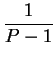獄中幻思錄---曹開新詩作品集, 曹開著,呂興昌編,彰化縣立文化中心編印,1999。
前言
這是為了配合康來新教授的教學需要而受她囑咐必須去讀的書。 書籍也是由康老師提供的。曹開是一位台灣籍知識分子, 白色恐怖的年代無端獲罪而入獄。不同於許多轉而化為一輩子抗爭的人, 他在出獄後並沒有涉足政治,也許他當初本來就是一介書生, 後來還是書生本色,因此他本來就不是因為政治狂熱而入獄, 那麼出來以後便以商養文,並不熱衷於政治。
以詩而言,曹先生的作品雖然在題材和內容上都很有創意,文字功力也還不錯, 但是可惜的可能是因為少年失學,只能在獄中從片段的文字中學習, 配以幼年接受中國標準入門典籍的庭訓, 因此氣度上還是在大雅之堂的邊緣。 不過,以業餘而言,算是傑出了。更何況體會此人一生之悲慘遭逢, 竟還以如此幽默之文句入於詩中,便更應當景仰此人。 但是,詩歸詩,人品歸人品,其現實就像政治一樣。 不過政治爭於一時,而文學留於萬世。 等到激情的時間過去了,真正檢視詩文的,仍是文學的眼光, 而非一個人當年的親身遭遇與時代背景。 在這個意義之下,我仍然要抱歉地認為, 曹先生的為人與生平故事理應受到時間的肯定而獲得後世讚揚, 但是他的詩,卻不太容易真正進入文學殿堂。
盡管如此,曹先生還是有不少佳作,值得在小地域、短時代內, 當作幾闕高級的作品來欣賞。 康老師和我總共在他的「數學詩」中, 選了九首當作大一國文與微積分協同教學的的教材,或準備教材。 這些包括
- 序詩二,小數點的詩感
- p. 57 徬徨的數字
- p. 60 數目的夢幻
- p. 64 獨裁的數學公式
- p. 78 三角形與圓形
- p. 81 幾何詩
- p. 89 演算:你加減我等於零
- p. 97 從零看人生
- p. 100 零超越宇宙
- p. 16 獄角的夜來香
- p. 10 鐐與銬
- p. 112 鐵鎚與鐵鉆的爭論
- p. 128 太空相思
- p. 166 陀螺比賽
- p. 172 無字天書
91 年 7 月份,我在漢聲電台的廣播節目中介紹了兩次曹開先生的詩, 後來又和主持人梅小姐就此製作了一份特別節目。以下先連結去兩份節目錄音, 您可以線上點播 (如果電腦中有 Microsoft Media Player 9 或者 Real One Player 的話),也可以訂購 CD 光碟 (一般的 CD 唱盤就可以播放):
事後,在 91 年 8 月,幾位英文系的學生將這兩天節目的「全文逐字稿」寫了出來。 我還沒有時間做任何後續處理,先將其逐字稿照樣刊登,有意者先取去用, 但是單維彰保留版權:- 漢聲電台 91 年 7 月 22 日廣播節目錄音--曹開詩集 (1) 逐字稿 (MS-Word 檔案)
- 漢聲電台 91 年 7 月 29 日廣播節目錄音--曹開詩集 (1) 逐字稿 (MS-Word 檔案)
教材文案:曹開與他的數學詩
中央大學中文系的老師康來新教授,在89年春天的一個早晨帶著通識中心的王燦槐教授和我, 一起出席漢聲廣播電台「校園開心講」節目。 當時她介紹了一位名叫曹開 (1929-1997) 的台灣詩人, 不過只有影印其中的一篇詩作來介紹而已。後來康老師找到了全集, 那是由呂興昌先生為曹開編撰的《獄中幻思錄.曹開新詩作品集》, 由彰化縣立文化中心出版,當時的縣長阮剛猛先生為它寫了序。 後來,民國94年,呂先生以《小數點之歌-曹開數學詩集》 為題在書林出版社再度為曹先生出版了詩集。
很多坐牢的人都認為自己是冤枉的,而各位要了解,就現在的情況來看,曹先生當時被關進去, 真的是頗冤枉的。而且不管怎麼說,他當時剛剛二十歲,由於政治因素被關到火燒島, 也就是我們說的綠島,在牢獄中渡過青春的十年。曹開生於彰化員林 (7月10日), 入獄前就讀台中師範學院三年級,在當時屬於較高的教育程度了。在呂先生所寫的序裡面看得出, 曹先生自幼學了一點中國古文,我們也可以從他的詩裡看到詩經、楚辭、古詩十九首的養分。 這些國學基礎現在來說或許很初等,但是在他所處的日據時代,能受到這種中國古文基礎訓練, 如果不是家裡有相當程度漢學知識背景的人,就是自修的成果了。 從他寫的詩句裡也偶爾看到徐志摩的影子,所以他也涉獵了一些近代白話文的創作。 康老師自己也說,純粹就文學的角度來看,其實這並不是個多有原創性的作者。 但是我們要了解那個時代的悲劇,有了那些背景以後,我們就能深切了解作者的可敬可愛, 以及他寫下這些文字的偉大之處。對於曹開先生,我們不能純粹用文學造詣的眼光來衡量, 而是要欣賞他在那個社會與歷史環境中所堅持的人性光輝。
在這本詩集所收集的照片中,最年輕的一張拍攝於1961年。當時待過綠島的人, 許多都是現在的大人物,但是曹先生並沒有。他獲釋以後,並沒有繼續在政治上發展, 或許他本來就不是在政治上有企圖的人。總之,曹先生出獄後,生活也是過得非常多采多姿, 他一定是個很聰明又活力充沛的人;在詩集的簡短介紹裡,提到曹開生活經驗豐富, 曾經經營果菜零售與批發生意、開設西醫房、皮膚肛門專科診所, 後來停業改經營房地產買賣及五金電器用品的切貨與批售, 退休後曾往阿根廷想要離開傷心地去養老,後來住不慣回來定居高雄。
其實曹先生在監獄內外,不曾發表地持續寫了三、四十年的白話詩,做了數以千計的詩篇。 他在1988年到澳洲旅行時,認識了宋田水先生。宋先生是台灣文學研究的一位長老, 他挑了幾首曹先生的作品,到處廣為介紹。呂教授得知後拜訪了曹先生, 深入地了解他的作品及他的一生,將所有陳年舊稿一篇一篇的看、一篇一篇的篩選出來百多首詩, 成為這本詩集,並將它們整理成三類。
呂先生所分的第一類是『獄中悲情』,紀錄他在獄中的所見所感。在這些詩中可以看出, 即使他面對如此不堪的遭遇也不怨恨別人,而是用一種很幽默的方式來對待別人, 更重要的是他也用相同的方式來對待自己。我讀書習慣都一頁一頁地翻, 即使讀詩集我也是一頁一頁地看。第一部份時己經很被感動, 很佩服曹先生在那麼糟的環境裡面,心裡滿受委屈,仍能用豁達的態度來看待自己的人生, 對待那些對付他的人,很少看到他寫出什麼怨懟的心情。
第二大類為數學名詞在字義上或數學概念上的聯想,最受呂先生推崇,他就稱之為『數學詩』。 他將數學元素注入新詩裡面,雖然只用了一些簡單的數學名詞,但那些意義也滿符合他的詩意。 這一部份的創作,可以說是用數學做為他創作的一個靈感源頭。
曹開寫出了很多關於數學的詩,其中可能還牽涉到一些高等代數的名詞, 相當於現在大學二年級,甚至更高年級才會學到的名詞。 我想像監獄裡的獄卒應該會不准閱讀才對,但是如果網開一面,獄政觀點中最「安全」的書籍, 恐怕非數學莫屬了。各位想想,在監獄裡讀數學,能做什麼? 所以獄卒可能就比較容忍曹開讀數學書,以聊解其鬱卒。不料他就算是讀了數學的書, 還是可以發揮他對自由的渴望,對未來台灣社會的憧景,以及對創作的熱情。 這說來有點黑色笑話。
當年康來新老師在廣播中介紹的那一首,就是被呂先生選為三首序詩的第二首『小數點的詩感』。 曹先生一直用小數點來稱他自己,而他的數學詩其實也有多處引用或闡述了小數點。
小數點的詩感
我一再的認證
我是人間方程式裡
最卑微的小數點
原無意投生在紛雜的函數中
你不必介意
更無需憐憫
你堅持你的算法
我維護我的向量
用四捨五入的定律
把我歸納留存也不錯
將我犧牲拋棄也無不對
在這加減乘除的公式中
清算競爭激烈的世界裡
我願承受無情的因式分解
按公理消去
彼此的恩怨
人人像數字
終結都得奔向無窮的零域
我將達觀的迎接
── 那盡頭的自由理想環!
這一篇詩裡的最後五個字「自由理想環」是一個高等代數的名詞。環 (ring)是一種代數結構,理想環 (ideal) 是一種次結構。不過自由理想環跟他前後文在數學意義上,毫無關係,純粹只是用了這個數學名詞,安插在這裡借用它的字面意義。望文生意,不要管他數學原來有什麼意思,就放到這首詩來看是很有創意的。
他一再的認證,他是人間方程式裡面最卑微的小數點,他原無意投身在紛雜的函數中。那紛雜的函數可能就是導致他入獄的事件。他當時是那麼年輕,你可以想像那正是很想表達自己想法的時候,可能就是因為多說了一些話,讓自己混在紛雜的函數中,結果就鎯鐺入獄了。
至少這本詩集裡蒐集的獄中詩,都展現對自己遭遇的豁達和客觀理解,好像在說,雖然我是個受害者,但是你也有你的苦衷。像這邊用了二句話:「你堅持你的算法」,要把我關起來是你計算的;但是「我維護我的向量」。此時「向量」就既有數學也有字面的意思了,就是我維持我的方向。
而我們也知道,小數點以下的數值可以四捨五入,你可以把它進位也可以把它捨去。雖然這個地方不完全合邏輯,因為不管你進一位還是捨去,其實那小數點都沒了,而他說你可以按照四捨五入把我歸納留存,這不完全符合算術的作法。當然我們也可以解釋說,我不在整數位做四捨五入,我在小數點以下第二位做小四捨五入,然後保留了小數點以下第一位和小數點本身。當然這樣繁瑣的解釋反而是沒有意思的!這四句是我覺得整首詩用得最適意的地方,因為寫詩如果全合了邏輯,那變成散文了。正因為這四句不合語法,才讓人讀了有一番感覺深入心裡。
如果要談台灣本土文學,曹開先生真的是非常地另類。而且他本是文藝界的圈外人,突然一下跳進來,等於是晚年才被發掘的奇葩。所以應該也要藉各種管道多多介紹一些他的作品。以下這一篇『鐐與銙』顯然被分在第一類。一共只有六句,而我非常非常喜歡這六句,覺得它真是黑色幽默到了極點。所謂幽默,其正解不就是以嘲諷的態度看待自己的不幸嗎?在這首詩裡,他不可憐自己,也不可憐別人,反而跑去可憐手銬與腳鐐,所以我覺得黑色幽默的厲害,這是真正高級的幽默。
鐐與銬
上面與你共戴的手銬
說是天空的比翼鳥
下面與我同繫的腳鐐
說是地上的連理枝
難怪鐐銬,一旦失去囚犯
一切感到唏噓,淒涼莫名
第57頁『徬徨的數字』裡,也同樣的用到了不少數學名詞。 有一些名詞是在詩裡跟數學裡可以有同樣的解釋。它也用到一個數學裡沒有的名詞「劫數」, 這是我們人人都知道的非數學名詞。
徬徨的數字
他像一個漂泊的數字
在一條不定方程式的兩岸
徘徊徬徨
因為經過整項分類
連自己也不知道
究竟屬於那種位階的數目
在清算紛雜函數的時候
他唯恐被代入消去法毀滅
他用代數歸納的語言
在 (括弧) 裡題上他的簽名:
「劫數」
然後,被因式分解而消逝了
雖然讀者可能不太懂什麼叫不定方程式,但是沒有關係,如果你看不懂數學的名詞, 從詩的角度你是可以體會的。此處的不定方程式也因為寫在詩裡,所以變得不是那麼合邏輯。 因為一方面好像是算術計算,另一方面又看得出來在做代數計算。
在國中我們學過 x、x2,我們也知道該怎麼處理同類項合併, 譬如如何變成完全平方,就用到了整項分類的技術。但在分類的時候,這個徬徨的數字, 卻不知道自己該屬於那一個位階的數,而說位階的時候又從方程式一下回到了十進位計數法, 究竟應該屬於十位、百位;還是十分位、百分位?它搞不清楚自己的位階了。 下一句又回到因式分解的寓意,在處理紛雜函數的時候唯恐被代入消去法裡面給毀滅。 消去法可能國中學生都還記得,假若等號兩邊有兩個式子,當我們要消去一個共同因式的時候, 要先確認等號兩邊都不是零,否則的話,我們就會犯錯。然後在 (括號) 裡面題了他的簽名, 這是我剛剛說的不在數學裡面的一個數,但是民間都知道的一個數:「劫數」。 最後這個徬徨的數字就被消去了
下一首用了更多的數,有一些數就像我們日常生活裡面講的,每個人都知道什麼意思, 另一些是數學裡面講的數,想像之豐富令目不暇給。很多數的名詞一個接著一個跳出來, 很漂亮地接在一起。
數目的夢幻
如今你異數 被套在 (括弧) 裡
動彈不得
那我因式分解
可以斷言一通
承前繼後,愛的方程式
永久有變數作隨從
恆遠有虛數
來把它服侍奉陪
它以美妙甜蜜的函數開始
卻往往要以劫數終結
凡情之所鍾,有貴賤的數目之差距
形成高下崎嶇的不等式
因此,永遠常數
敵不過變數
虛數戰勝實根
真數敗給劫數
無理數打贏有理數
零凌駕無窮大
圓卻變成了
偽自由理想環
如今你異數被括在 (括弧) 裡,被關在監牢裡,它的排版很有趣, 括弧的兩個字的外側還畫了兩個括弧符號,就是監牢的意思。「我因式分解,可以斷言一通」。 我不太了解這一句什麼意思,不過可以感受或許有一點抱怨吧,抱怨把他判了刑, 關在監牢裡面。不過這後頭大部份都還滿甜蜜的,「承前繼後,愛的方程式, 永久有變數作隨從,恆遠有虛數,來把它服侍奉陪」。「它以美妙甜蜜的函數開始, 卻往往要以劫數終結,凡情之所鍾,有貴賤的數目之差距,形成高下崎嶇的不等式」。 最後這一句很美妙,高下崎嶇的不等式。而後面接的部分讀起來可能會覺得有點繞口, 這可能是斷句的問題。零跟無窮大是哥倆好,常常是一對,或者有時候把它們當作一樣的, 譬如說在投影幾何裡面。在某種抽像的概念裡,是把最遠跟最近當作同一個位置來看待。
「常數敵不過變數」,這沒有什麼數學上的意義,不過這兩個詞這麼放在一起,滿好看的, 有對仗的美感,有我們生活上可以理解的意義。「虛數戰勝實根」, 這個地方我認為不太好,我不知道他為什麼要加個實根,也許加個實根是想變化一下, 避免連續寫兩個「數」。實根就是滿足多項式等式的實數。例如多項式方程式 x2+1=0,那 x 要代進去什麼數, 使得 x2+1=0?代進去使等式成立的數,就叫做這個方程式的根。 但如果我說 x2+1=0 的話,那麼它有二個根:一個正 i, 一個負 i,其實就是虛根。但若是 x2-1=0 的話, 就會有二個實根:一個正 1,一個負 1。 這個地方我想跟前面常數敵不過變數一樣,沒有什麼數學上的意義, 就是利用數學的名詞作為一個對仗。
後面一句對仗得也很漂亮:「真數敗給劫數」。因為真數跟劫數都不是數學裡面談的數, 所以也就不必解釋了。連續這四句,都是常規的敗給混亂的,講理的都輸給不講理的, 所以「無理數打贏有理數」就說得太白話了一點。「零淩駕無窮大」, 在前面我已經闡述過了。在很多數學的結構裡,的確把零和無窮大視為同樣的東西, 的確是這樣子的。以數學眼光來看的話,當然是沒有太奇怪,但是以社會上的眼光, 這當然是太奇怪了,零怎麼可以在無窮大的上面呢?
「圓卻變成了偽自由理想環」就是理想的幻滅。這其實是一個很抽象的數學結構名詞, 我想我們不深究這個道理的話,就是直接藉由這五個字放到這個地方來。 我猜想他在監獄裡面一定讀到高等代數了,他讀這些數學的書, 很有可能目的也不是讀數學,他是個文化人,就是想要看書而已。 他是不是真的懂了什麼是群、環、體?是不是真的了解到可以做出習題的地步? 我們不知道,也許他雖然讀的是數學書,但是他學的還是裡面文字給他的啟發。 所以他後來做的是詩,而不是數學(歷史上的確有好幾個在監獄中完成的數學)。
『獨裁的數學公式』是我非常非常喜歡的一首詩。不僅詩意表達得很棒,數學也用得很正確。 如果說這整本詩集只讓我講一首詩的話,站在數學老師來談曹開先生的立場,我應該挑這一首。
獨裁的數學公式
人間繁分式裡
他構造一條倒函數
成為
P = People 代表人民
在專制的公式裡
盤鎮於最高層的寶座上
傲視下界威風凜凜
獨一無二就是至尊的象徵
而當 P 值趨向無窮大
他的價碼趨近零
要是 P 值趨向極小
他乃形成負面的數目
第三句將獨裁寫成數學公式的樣子 1/(P-1)。分母 P-1 寫在下面,上面的 1 淩駕一切, 而 P 是所有人,減1是扣掉他自己。全世界的人除了他自己以外,全都在他下面, 這 1/(P-1) 用得很妙。獨裁的寡頭在分子,也是這個國家裡面所有人民中的一個, 但他跟別人不一樣,他在社會的上面,在法律的上面, 「傲視下界,威風凜凜,獨一無二,是至尊的象徵」。最後四句又真的是妙極了, 此 1/(P-1) 分數,就當 P 是 11 好了,1/(11-1) 就是 1/10,也就是 0.1; 這 P 如果是 101,1/(101-1) 就是 0.01。 所以學過微積分或中學基本極限概念的人會有這個概念:1/(P-1) 的 P 在分母, 如果 P 愈來愈大,那分母會愈來愈大,則整個數值會愈來愈小。所以當 P 值趨向無窮大, 他的數值趨近於 0。這個地方帶有點詩意,而且這個詩意用的是正確的數學意思。
就詩意來說,當人民的意識愈來愈強時,做一個寡頭就越來越困難,所以他的價碼就愈來愈低, 最終總有一天會被推翻;而人少的時候雖然他比較控制得住,但是如果P值太小了, 譬如說小於 1,如 0.2、0.3,那麼 P-1 變成一個負數,則他的價值反而會成為一個負面的值。 其實說不定數學裡的詞彙本來就有詩意,只是我們看慣了,比較沒有感覺了。 總之,這一首詩裡衍生出來的意義,即獨裁者碰到有公民意識的人民以後就會被推翻, 他的價值愈來愈低。但是人如果太少了,雖然管得住卻也管得沒意思, 獨裁者總是希望自己的權利越多越好。當然被管的人多,他的權利就愈多, 可是人多了他就會跨掉,那人少的時候獨裁者就會覺得無法滿足他的欲望。
分析數學
數對括弧說:
「你是我的」
括弧便把數禁在鐵匣裡
點對面積說:
「我歸你的」
面積便賜給點
在軌跡上的自由
這首詩非常有趣。第一個有趣的地方是,這首詩的內容和它的標題是完全相對立的。 這首詩的標題叫分析數學,分析數學看在數學人的眼裡是件嚴肅的事情, 即使看在不是數學人的眼裡,你也會覺得有點冷陰陰、高不可攀。數學已經夠可怕了, 還要分析數學。可是這裡面說的雖然有數、有點、有面積,看來像是幾何和代數都有, 但是明明是一首情詩。「數對括弧說,你是我的」這個邏輯,下一句話說, 「括弧便把數禁在鐵匣裡」,這不是一首情詩嗎?
其實我的感受是另外一種,這個情詩在反應一個不成熟的愛情。 一個不成熟的愛情說你是我的,我要佔有你,你是屬於我的。可是當一個不成熟的愛情發生, 且我在佔有你的時候,可是被禁錮的是我自己。「數對括弧說,你是我的」我擁有你, 或者你屬於我,那個括弧卻把數給括起來了。反過來說,一個成熟的愛情, 就像點對面積說「我歸你的」,我沒有要你屬於我,面積就賜給了點在面積上的自由, 這是很棒的一個情況。
談到這裡,我想跟很多大學一年級要開始談戀愛的同學說, 當你交了男朋友或女朋友之後,哪一天你稍微要留意一下,當你交了這一個人以後, 你的朋友群是變多了還是變少了。常常,一個人交了異性朋友以後,就失去了所有的朋友, 你的生活圈子裡面就只有那一個人。這樣甜甜蜜蜜了三年、四年後,通常都會分手, 我很少看到成功的。分手以後,你會覺得回想起來,在這大學四年我沒有認識什麼人, 我沒有跟很多人談過話,我完全沒有接觸過另外一種思想、興趣或者是生活, 好像這個數在括弧裡面一直沒有逃出來過。很多人都有這樣的經驗,後來很後悔, 但是已經來不及了,你最多采多姿的那幾年已經結束了。所以好的男女朋友感情, 應該是我交了這麼一個男朋友、女朋友以後,讓我們兩個的朋友多了一倍。 這時候你就開展你的生活圈子、你的視野。剛談戀愛的人喜歡擁有別人, 同時還要被別人擁有,如果他沒有被別人擁有,還會不高興。他喜歡被別人管得緊緊的, 有的時候你給他太多自由,他還會認為你不愛他。所以我說這首詩很有趣。
下一首介紹『三角形與圓形』。這首詩非常有創意,你得用眼睛看,因為它需要配合一張圖。 我們先複習一點點國中的數學。正三角形每個邊都一樣長,每個角都是60度。三角形有六個心, 我們現在只談一個心:重心。我們想像一個三角形的板子,用一種材質均勻的質料切割出來, 稍微有一點厚度及重量,當你的手指頭撐著三角形某一個點的時候,它恰好達到平衡, 那個地方即是重心。三角形的重心差不多在整個三角形的正中央。以三角形而言很簡單, 在每一個邊取它所謂的中點,中點與對面的點連起來,三條線很巧妙地會交於一個點。 我們知道平面上兩條線如果不平行的話,會交於一點,而此處第三條線也會交在同一點, 這是一件巧妙的事情。
接著我們複習圓,圓是以一個圓心、一個半徑長度畫出來的。而三角形與圓有一些簡單的關係, 這個圓可以嵌在三角形裡面,圓恰好和三角形的每個邊相切,剛剛好包在裡面, 我們稱之為三角形的內切圓;另外一種情況是圓在三角形的外面,三角形被包在裡面, 三角形的點沒有刺穿出來,剛好讓圓通過它,三個頂點正好接在圓上, 我們稱之為三角形的外接圓。
三角形與圓形
這是他倆的寫照
[一張圖:正三角形和它的外接圓]
尖尖銳利的三角形
和溫柔的圓偎依在一起
圓肯以三角的重點
做為自己圓規的中心
圓周和順的貫通
尖銳的三角頂
這是典型的愛情公式軌跡
自古遵循的定律
看!圓與三角形團聚
雖他倆形狀迥異
似格格不入
但他倆卻能鍥合同心
融洽似夫妻
這裡看到一個很尖銳的人,通常是老公,被另一個很溫柔很圓滑的伴侶,通常是老婆,包著。 詩集的下一頁又有一首非常類似的詩,這一次曹開只寫了四句。
幾何詩
方與圓 似剛與柔
圓合於方
方鍥合於圓
兩心同一點
這首『幾何詩』並沒有配圖,但也可以使用前面的圖。 我們既然能夠了解正三角形可以嵌在圓裡面,相同的正方形也可以嵌在圓裡面, 或者說正方形可以包在圓的外面。而且當你用正方形跟圓互相包的時候, 他們的重心跟圓心亦是同一點。曹先生用了兩個幾何上面的現象,做出了這兩首詩,一長一短。
接下來的兩首詩都與零有關,寫得越來越超脫。第一首,短短的八句。
從零看人生
零,虛懷若谷
面對世界的
加減乘除的清算
不做無謂的爭執
它給與人類
圓滿的修行啟示
提升人生
達到無我的最高層次
這首其實有點不像詩,有點像是禪機偈語。「零,虛懷若谷, 面對世界的加減乘除不做無謂的爭執」。我們知道,零配到加、減不會影響原來那個數, 配到乘會變成零,除時,要看零在分子還是分母。不過不用這麼認真解釋。總之, 零和其他數做加減乘除的時候,結果很單純。所以詩中才說,不做無謂的爭執。
零超越宇宙
零是無邊無際的總和
它是宇宙之母
從它的胎盆
萬物產生
它是中立的樞紐
不偏袒任何方位
積極而不孤零
統合一切,調和虛實
零樂觀的參與
操作所有的轉機
創造世間
脫俗的內涵
只有零能令狂妄的無窮
回省歸元
渺茫自大的太極
收斂知還
這首詩後面的幾句很妙。零,真的是太道家了一點。「渺茫自大的太極,收斂知還」,知道自己的本位。我不確定曹先生這邊究竟想要表達什麼領悟的道理,但是覺得這幾句話,讀起來滿美妙的。所以這首詩,可以拿來代替他前面所寫的「提升人生」達到無我的層次。到底提升了什麼?他給予人類圓滿的修行啟示,啟示零能夠讓狂妄的無窮回歸到本來的面目。
如果我們用數學的觀點,這是很多學生犯的錯誤:以為零乘上無窮大就會是零了。 其實零乘上無窮大不見得是零,也不見得是無窮大。零乘上無窮大稱做不定型式, 什麼都有可能,它可以是 1,可以是 2。這樣的題目與計算問題,可以隨意去設計答案, 這是在微積分中應該了解的事情。但是詩人將它用在這個地方,顯然他認為, 零是無邊無際的總合,它是宇宙之母,「零樂觀地參與操作所有的轉機,創造世間脫俗的內涵」。 表面上的解釋是,零在表達數字上是非常重要的,如果沒有零, 你不能夠分辨 50 和 500 有什麼不同,除非你要寫出中國字五十或是五佰出來。 但是如此的記數法用來做加減時是很困難的,所以零是一個很重要的記數符號。 當我們從小學做直式加減乘除的時候,零都非常的重要,一旦擺錯就會算錯。
在曹開詩集中,一再提到零與無窮大是一種對比,或是類比。它有真正的意思, 在數學邏輯上,或是幾何中有合理的解釋,所以可以說零操作了所有的轉機, 創造世界上所有脫俗的內涵。我不太相信曹開先生真的知道他恰好寫出來的數學意義, 就像有一位外國的學者說,西達多在菩提樹下所參悟的道理, 超過所有物理學家用精密設備所知道的自然現象。但是也有物理學家認為, 必須要透過精密的測量計算,觀察和反覆的實驗才能夠歸納而創造定律, 不管你有多聰明,光靠冥想是不夠的。曹開先生用他的人生經歷, 純粹靠內省所創造出來的一句話:零創造世間脫俗的內涵,恰好在數學上有其意義。 數學中的 1、2、3、4 是不能夠用任何物質來定義的,而是從零開始的。 那零怎麼跳到 1,零就是沒有,怎麼可能跳到 1?這是從集合論來探討的, 零可以對應於一個空集合,利用空集合製造出一種集合,可以對應1的這個觀念。 而加和減的運算都變成集合的運算,所以在完全不依賴任何物質的情況下, 把零定義出來,接著把 1 定義出來。有了 1 以後,後面所有的正整數都可以定義出來了。 這就是數學家利用零所做的創造。
西方也有人將數學入詩,我在留學的時候見過零零星星幾篇,沒有收集成冊的。 例如數值分析領域有一位 Falk 教授,在圈子裡面是有名的詩人。 我曾經看過他即席隨興的創作,也因此知道他一些其他的作品。 數學家寫詩大概都是遊戲作品吧,不是很認真也沒有想要發表, 都是數學家之間寫來自娛娛人的。在台灣也一樣, 我起碼讀過王九逵、李國偉和方元教授的詩作,但是從來沒有聽說哪位同行有正式發表詩作的。
接下來再補充一句話。在學校裡面參與創意教學的工作,我想要強調的是,創意不是一個點子而已。創意是先有一個點子,然後抓住它,然後一直朝完美的方向做。而沒有做完的事情,不算有創意,憑空亂想但是不做出來就不算是創意。而且每一個細節都要顧到,要不然你就是在浪費自己的點子,你做壞一個點子就是浪費一個點子,不能再做第二次了。因為不論是你自己還是其他人,只要是第二次就被認為是沒有創意的,有創意的人是不會去做的。所以被你浪費的點子,就是永遠地被毀壞掉了。因此,有了那麼一個點子的時候,要珍惜它、抓住它,然後一直持續、有耐心地做下去。
最後我想介紹黃久晏同學寫的一首數學詩,做一個小小的對照。久晏是中央大學數學系91年入學的學生。她或許是在讀微積分讀得很快樂或是很不快樂的時候,寫下這首詩的。我個人覺得她寫得滿恰當、滿可愛的,當時她十八歲。我要感謝康老師,或許就是因為她在數學系的國文課裡介紹了曹開的詩,刺激了這位數學系的女生產生這首作品。她還紀錄了日期:5月30日,大概她正好學到重積分的地方。在曹開的詩裡面,你看到代數類最高等的名詞就是理想環,而分析類其實就看到極限而已,看來曹開他似乎沒有讀到微積分。
暗戀
我用微分接近你 你用積分再積分疏遠我
我們之間的距離也許早已過了拋物線的最高點
或許泰勒說的對
n 的值取決於你的心意
遙遠遙遠,你未曾正視我一眼
n 趨近於無窮大
Dn 也趨近於無窮大
我只能沈默、沈默,像一個失去重心的橢圓
不停地繞著傷心打轉
太多變數,太多因數
愛情是一條無解的函數
性別不同,生命的經歷也不同:黃久晏跟曹開同樣二十歲的時候,一個在牢裡,一個正是幸福的大學生。但是我覺得黃久晏這首詩有些部分用數學用得蠻好的。「我用微分接近你」有小小步、小小步慢慢靠近的感覺。「你用積分再積分疏遠我」,我剛剛說她可能正在學重積分,重積分就是要積分再積分,愈積愈大,她的感覺是愈積愈遠。然後已過了拋物線的最高點,我想大家都知道這是什麼意思。
泰勒,也是他們正在學微積分的主要課題之一,也就是泰勒展開。 她說「n 的值取決於你的心意」,當然我相信這不是泰勒說的,不過這邊詩意滿好的。 「你未曾正視我一眼,n 趨近於無窮大,D of n 也趨近於無窮大」,老實講, 我不知道她的 Dn 是什麼東西,很可能如果她指的是泰勒展開的誤差項的話, 如果 n 趨近於無大,這個誤差項應該要趨近於零, 代表最後逼近的曲線跟原曲線要完美的落在一起,完美的疊合在一起。 但現在這個不幸的情況是,n 趨近於無窮大的時候,誤差項 D of n 也趨向無限大, 那就沒有希望會收斂了。這個多項式,或說這個級數將不會收劍到我們想要靠近的那個函數, 這是滿可悲的。
最後她只能沈默,就像一個橢圓,不停地繞著傷心打轉。這很棒,重心是科學名詞,傷心是文學名詞,把兩個放在一起。接著太多的變數,太多的因數,雖然並不完全是同音(因素),但是滿押韻的。「愛情是一條無解的函數」,其實我現在覺得是一條無解的曲線會比較押韻一點。所以顯見十八歲是可以多讀些東西的時候,多努力地在腦筋裡有意識的去創作,不要無意識地等待靈感來臨。
[曹開數學詩 MS-Word 版本 97KB]