質數魔力 (上、下), Derbyshire, 陳可崗譯,天下文化【科學文化121,122】2005, ISBN 986-417-598-X
我在 2006 年初跟《科學月刊》領了這兩本書,自願要寫書評。 其實在四月中旬就讀到第 19 章了。 因為某個突發的原因暫時擱置,一擱就到了 2007 五月。 越是重要的事情,總是被拖延到越晚,因為我希望認真投入時間去閱讀和思考。 我甚至很希望能親自寫程式去算算看。所以拖延了許久。
有人敢用黎曼猜想作為科普的題材寫書,實在是個很有勇氣的選擇,而且想必充滿了熱情。 這也是我很好奇的課題:一個複變函數的根是怎樣和質數扯上關係的? 不要說是它的證明了 (反正還沒出現),就連它的題目我都不懂。 雖然這件事跟我的工作與生活都毫無關係,但是真的很好奇而想要學習! 曾經想要認真去了解這個問題,向同事夏良忠教授借來一本書, 甚至計畫著按圖索驥親自寫程式去計算看看。 可是其他的事務纏身,居然連那本薄薄的小冊子都沒有讀完, 就因為夏教授需要用而歸還了。
作者果然充滿了熱情,就連譯者也是。 陳可崗先生寫的『譯後感』就可以當作這本書的簡介 (上冊 p.227)。 節錄一段他的原文:
作者要表現的是一百五十年來數學家「擺脫不了對質數定理與黎曼假設的思索, 和對黎曼本人的感情」。這整本書是循兩條敘述的軌道進行:奇數章敘事---數論、質數定理、黎曼假設等等; 偶數章敘人---黎曼、黎曼之前的數學家、黎曼之後的數學家、 研究黎曼假設的近代數學家,以及各時代的歷史地理背景。
原來數論也是一個饒富趣味的領域,如果我們要問,數論有甚麼用, 沒有人能指出它的立即用途。可是你若是以「益智」為目的, 以拓寬知識的視野為動機,讀本書會讓你感受到那扇標示「數論」的窄門, 打開來一看,裡面竟是一片花團錦繡。
一個無窮級數
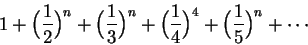
的 n 一般只有做為整數來討論:若非等於 1,就是大於 1; 前者為發散,後者為收斂。殊不知 n 還有可能是一個複數,當 n 是複數時, 這個無窮級數就叫做黎曼的「zeta函數」,其中藏有無窮的奧妙。
前面那個無窮級數,用 L(n) 表示它,是怎樣和質數扯上關係的?因為
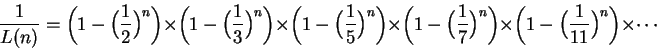
等式左邊是個分數,分子是 1,分母是前述無窮級數; 等式右邊是依序採用質數 (2,3,5,7,11,...) 寫成的無限連乘。 作者為我們做了些研究,找到歐拉 (Euler) 的原始證明 (只有十行德文), 放在第七章第三節 (p.144 起)。 歐拉有許多非常美妙的證明,都因為「不夠嚴格」而無緣進入現在的正規數學課本。 我非常感激作者挖出來這個真的很簡單的證明; 科普書嘛,別去管嚴格了,如果歐拉能夠接受它,我們也可以接受。
到這裡,讀者應該明白我在前面說作者「很有勇氣」的原因了: 這個題材有兩個線頭,一頭是質數,這個相對比較容易, 但是另一頭必須從無窮級數開始,這就意味著以微積分為基礎, 然後複數也必須進場,就這一點來說,甚至超出了大一微積分的範疇。 如果這些還不夠把讀者嚇走,他居然再把「證明」放到科普讀者的面前(例如前段所述)!
如果讀到這裡您還沒有被嚇到,反而覺得躍躍欲試,這本書就是適合您的了。 上冊的命題是「質數定理」,但是已經在為黎曼假設鋪路, 而這一冊可能比較接近一般數學科普讀者對於一本書的預期。 下冊的命題就正式是「黎曼假設」了,這一冊的後半本可能需要更多的背景知識或耐心。 如果失去耐心,可以直接跳去最後一章。
對我來說,閱讀這 (兩) 本書是個非常愉快的經驗。 作者想必知道,他所描述的數學家 (特別是黎曼以前的那些人) 都是科普書籍中的經常性主角,所以他選擇放在這本書裡「敘人」的那一部份, 除了基本資料當然要重複以外,的確是比較特別而少見於其他讀物的故事。