永無止境的改進

如果要我冒著被指責為膚淺的風險，用一句話說明微積分是甚麼，那就是：經由對『無窮』的理解與掌握所發展而成的一套超級計算方法。捨棄數學課本的嚴謹標準，讓我們以科普的標準來闡述這個說法。但是面對《科學月刊》的讀者，這個標準當然還可以更高一點。就從二項式展開切入吧：，，。把 (x+1) 的次方展開之後，按照 x 的次方排序，那些係數就形成所謂的巴斯卡三角或楊輝三角 (最近聽李國偉教授說，其實楊輝的書裡明明說那是賈憲做的，所以該叫『賈憲三角』才對)。用組合數的記號來寫，就像是
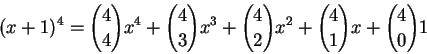
$\begin{displaymath} (x+1)^4={4\choose4}x^4+{4\choose3}x^3+{4\choose2}x^2+{4\choose1}x+{4\choose0}1 \end{displaymath}$

應該所有人都看出規則了，以上規則可以推廣成任意的正整數次方，為了避免更多數學符號，就不寫了。而組合數的計算規則，就是根據上方和下方兩個數，形成一個分數。分子是從上方的數開始，連續乘每次減一的數，總共乘下方指定的個數；分母是從 1 開始，連續乘每次加一的數，總共跟分子乘同樣多個數。例如
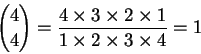
$\begin{displaymath} {4\choose4}={4\times3\times2\times1\over1\times2\times3\times4}=1 \end{displaymath}$

而
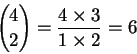
$\begin{displaymath} {4\choose2}={4\times3\over1\times2}=6 \end{displaymath}$

當下方是 0，分子和分母都沒有數，當作個案處理，規定那種組合數都是 1。奇妙的是，只要上方和下方都是正整數，組合數的分母都會整除分子，而得到整數的結果。我們就別岔開話題了。
按照組合數的遊戲規則，只要上下方都是正整數而且下方比較大，結果就是 0。例如
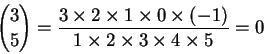
$\begin{displaymath} {3\choose5}={3\times2\times1\times0\times(-1)\over1\times2\times3\times4\times5}=0 \end{displaymath}$

道理很簡單，在這種情況，分子總會遇上一個 0，而只要有 0 出現在分子，整個分數就是 0。所以，其實二項式展開本來有無窮多項，只是恰好多出來的都是 0 而已。例如
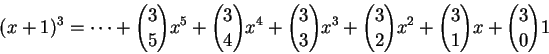
$\begin{displaymath} (x+1)^3=\cdots + {3\choose5}x^5+{3\choose4}x^4 +{3\choose3}x^3+{3\choose2}x^2+{3\choose1}x+{3\choose0}1 \end{displaymath}$

但是如果上方不是正整數而下方還是正整數 (或 0)，組合數的遊戲規則還是可以玩下去，例如
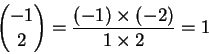
$\begin{displaymath} {-1\choose2}={(-1)\times(-2)\over1\times2}=1 \end{displaymath}$

而
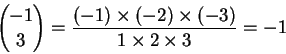
$\begin{displaymath} {-1\choose3}={(-1)\times(-2)\times(-3)\over1\times2\times3}=-1 \end{displaymath}$

對於上方是 -1 的組合數，有個簡單的規則：當下方是偶數時，答案是 1，否則是 -1。把這些組合數『盲目地』套進二項式展開的公式裡面，那豈不就是說
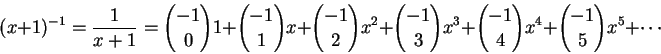
$\begin{displaymath} (x+1)^{-1} = {1\over x+1} ={-1\choose0}1+{-1\choose1}x+{-1\choose2}x^2+{-1\choose3}x^3+{-1\choose4}x^4 +{-1\choose5}x^5+\cdots\end{displaymath}$

現在我們依照數學式的習慣，把表示無止境繼續下去的 $\cdots$ 寫在式子的後端。代入那些組合數的值，就是
$\begin{displaymath} (x+1)^{-1}=1-x+x^2-x^3+x^4-x^5+\cdots \end{displaymath}$

好一個漂亮的等式啊！可是，這樣盲目地亂套公式是可以的嗎？在牛頓那個時代，這些震懾心靈的發現一再出現，絢麗而令人迷惑。我們跳過那兩百多年的歷史，就說如果將 x 代入不超過 1 也不小過 -1 的數，那個無窮的二項式展開是對的。如果讀者看得出來等號右邊是以 -x 為公比的無窮等比級數，就應該知道在前述範圍內收斂到 1/(1-(-x))，也就是 (1+x)^-1。即使您看不出來，相信也能體會，當初發現這個秘密的時候，心頭上興奮到甚至於感到恐慌的那種情緒。
這條牽涉到無窮多個數相加的等式有甚麼『意義』？顯然我們沒有能力計算無窮多個加法，所以這種等式究竟有甚麼用？當然是有用的，否則微積分就不會被認為是科技文明的基石了。這種等式帶給我們的，並不是需要無窮多次計算的負擔，而是永無止境的資源！如果我們的需求不高，可以只計算前三項而得到一個接近真實答案的結果。如果對答案的精確性有更高的需求，就再多算幾項。需求更高，就算更多。無論我們提出多高的需求 (總不會是『無窮高』嘛)，那條等式總有更多的項目讓我們計算，而滿足需求。這種有無窮多項的等式，讓我們有取之不盡的資源來永無止境地改善計算的精確度。
讓我們將 x 代入 1/2 試試看，等式的左邊是循環小數 $2/3=0.666\ldots$ 。如果右邊只算三項，得到 3/4=0.75 當然不夠準確。但是如果計算九項，就大約是 0.66602，有三位準確數字了。如果計算二十項，大約是 0.66666603，準確到第六位。算越多項，準確的位數就越多，而我們永遠不愁沒有下一項可以算。雖然這個計算永遠不會真正等於 2/3，但是在實務上，我們只需要差不多的結果。 0.666666*3 是 1.999998，與 2 只有 10^-6 的相對誤差，對大部份的實務問題都已經夠準確了。如果還不夠準，那就再繼續算吧。
當然我們不會真的用這個超級工具來計算 2/3。把次方從 -1 換成 1/2，那就是
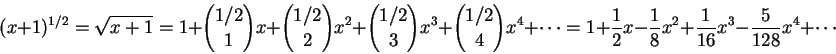
$\begin{displaymath} (x+1)^{1/2} = \sqrt{x+1} =1+{1/2\choose1}x+{1/2\choose2}x^2+... ...=1+{1\over2}x-{1\over8}x^2+{1\over16}x^3-{5\over128}x^4+\cdots \end{displaymath}$

用它來表演計算 $\sqrt7$ 的一種方式。因為代入的 x 必須介於 $\pm1$ 之間，而且它越靠近 0 越好 (這樣會更準確)，所以我們用 7=9-2=9*(1-2/9) 這個技巧，將 $\sqrt7$ 看成 $3\sqrt{1+(-2/9)}$ 而將 x 代入 -2/9，算出結果再乘以 3。計算前二、三、四、五項的結果依序大約是 2.666666, 2.648148, 2.646091, 2.645805。觀察這些數字的變化趨勢，會發現隨著計算項目的增加，前幾位數字開始不再改變。那些不再改變的部份，就肯定是正確的數值。算的項目越多，不再改變的位數就越多，我們也就得到越多的正確數值。即使我們不知道真正答案，也看得出來，前三位肯定是 2.64，而如果要猜第四位的話，應該是 5。 2.645² 大約是 6.996，與正確的 7 只有 0.06% 的相對誤差。如果您不滿意，就繼續算吧。
$\sqrt7$ 是個無理數，本來就無法完整寫出它的小數部份。因此，使用無窮多項的計算方法就恰如其分。算的項目越多，就得到越多肯定的數值，也就是越精確的意思。這種無窮多個數相加的算式，稱為無窮級數，它是微積分那套超級計算法裡面的一員大將。這又跟過去三個月我一直在談的指數與對數有何關係？且看下回分曉。

[ 回上層 ]

Back to the home page of Wei-Chang Shann.
Connect to the home page of Department of Mathematics, National Central University, Taiwan.

shann@math.ncu.edu.tw