從武士刀到毛瑟槍

話從五月號專欄休止的地方接續起，高中數學課本裡面的三角函數表，是怎樣算出來的？其實在電子計算器這麼方便的時代，三角函數表本身已經是歷史，它的製作方法也許更接近歷史課題，而不是數學課題。不過，任何一個嚴肅的學習者，不論在哪個科目，都應該對學科的歷史有基本認識，不是嗎？而我講這段古的目的，倒不是想要揭開歷史的面紗，是想要提昇讀者的鑑賞力，提高您的閱讀樂趣。至於嚴肅的教材，推薦您看蔡聰明教授發表在《數學傳播》卷 90 (1999) 頁 57--67 的『星空燦爛的數學---托勒密如何編製弦表』。
托勒密 (Ptolemy, 100--178) 是希臘文明末期的博學之士，畢生主要工作之一是天文學，所以前述文章會以『星空燦爛』為題。為了天文測量的計算，他製作了相當於「解析度」為 $\frac{1}{4}^\circ$ 的正弦函數表：也就是角度為 1/4 的整數倍的正弦函數估計值，例如 0.25, 0.50, 0.75, 1.00, 1.25, 1.50 等等。如果每個估計值都準確到小數點下第四位，我們說這張數值表的「精確度」是 $10^{-4}$ 。托勒密當時使用的是 60 進位的記數系統，而且沒有小數記法，只有分數，所以並不容易用今天的詞語定義他那張表的精確度，故省略不談。
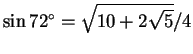托勒密時代的學者已經熟知 30, 45, 60 這三個特殊角的正弦比值，也就是每個高中生都知道的 1/2, $\sqrt2/2$ 和 $\sqrt3/2$ 。圓內接正五邊形的幾何作圖法，可能早托勒密五百年就已經在希臘的知識庫裡面了，收錄在歐幾里得《幾何原本》第四卷之中的命題 11。從這裡可以導出 72 度的正弦比值 (當然 18 度和 36 度也都順便可得)。許多高中生可能背得出來 72 度的餘弦比值是 $(\sqrt5-1)/4$ ，而這個數恰好是黃金比 $\phi=(\sqrt5-1)/2\approx0.618$ 的一半 (那個希臘字母的讀音像ㄈㄧ)。現在的學生不必跟隨歐幾里得的嚴格推理路線，直接從底角為 72 度的等腰三角形出發，透過相似三角形的邊長比例關係，就能得到 $\cos72^\circ=\phi/2$ 。再經過畢氏定理 (所謂的平方關係) 得到 $\sin72^\circ=\sqrt{10+2\sqrt5}/4$ 。從和差關係
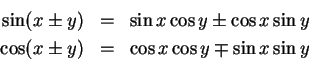
$\begin{eqnarray*} \sin(x\pm y)&=&\sin x\cos y\pm\cos x\sin y\\ \cos(x\pm y)&=&\cos x\cos y\mp\sin x\sin y \end{eqnarray*}$

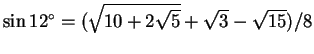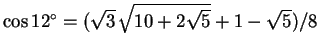可以利用 $72^\circ - 60^\circ$ 得到 $\sin12^\circ=(\sqrt{10+2\sqrt5}+\sqrt{3}-\sqrt{15})/8$ 以及 $\cos12^\circ=(\sqrt3\,\sqrt{10+2\sqrt5}+1-\sqrt{5})/8$ 。利用 x=y 的特例得到兩倍關係
$\begin{displaymath} \sin 2x=2\sin x\cos x,\quad \cos 2x=\cos^2x - \sin^2x \end{displaymath}$

以 12 度為已知，代入 x=6 度可以求解 6 度的正弦比和餘弦比；再以 6 度為已知，代入 x=3 度可以求解 3 度的正弦比和餘弦比。這些數已經複雜到連排版都累。現在，將和差關係中的 y 代入 2x，利用平方關係化簡得到三倍關係 $\sin 3x=3\sin x-4\sin^3x$ 。以 3 度為已知，代入 x=1 度就成了
$\begin{displaymath} 3(\sin1^\circ) -4(\sin1^\circ)^3=\sin3^\circ \end{displaymath}$

所以 $\sin1^\circ$ 就是三次方程式 $3x-4x^3=\sin3^\circ$ 的一個正根。
三次方程式在這裡出現了，這可能是人類文明跟三次方程式的第一次「遭遇戰」呢。寫成標準式 (本欄六月號) ，則 p=-0.75 而 $q=-\sin3^\circ/4\approx-0.0131$ ，這是一種有三個實根的狀況，其中靠近 0 的正根為所求，大約 0.0175。有了 1 度的正餘弦比值之後，再用兩倍關係，兩次，就抵達 1/4 度了。一張以 1/4 度為解析度的三角函數表，就從這裡開始建造。如果要提高解析度到一分，也就是 1/60 度，那就依此要領繼續努力吧。
讀到這裡是不是已經要發脾氣了呢？其實這就是目的：經過這樣的煎熬，才能體會等一下浴火重生的喜悅啊。在微積分提供了無窮級數這種工具以前，從托勒密一直到十六世紀，基本上就得使用上述辦法來計算三角比值。讀者此時應該可以想像那份工作的龐大，於是可以理解，為甚麼在歐洲的航海時代，需要以「傾城之力」來製作解析度和精確度都更高的三角函數表。
有了微積分又如何呢？這套超級計算法提供了一個有系統的方法，將難計算的函數轉化成相對來說容易計算的多項式。像 , 和這樣的式子叫做多項式，此處所謂的計算，只是將 x 代入一個數，例如 x=0.7854，算出多項式的數值。當函數具有某種好的性質，用來估計它的多項式次數就能無上限地提高，而成為提供無限資源的無窮級數 (本欄一月號)。請觀察以下等式
$\begin{displaymath} \sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}-\cdots \end{displaymath}$

相信任何人都看得出規則了；其中 n! 表示從 1 到 n 的連乘積，例如 3! 表示 $1\times2\times3=6$ 。可是那條等式必須以弧為單位，理由寫在本欄五月號的最後。例如代入 $x=1^\circ=\pi/180\approx0.0175$ ，則只根據級數的第一項就得到 $\sin1^\circ\approx0.0175$ 等於我們前面求得的估計值！如果用 $10^{-10}$ 的精確度做計算，則只要計算前兩項 (三次多項式) 就能得到 $10^{-10}$ 精確度的 $\sin1^\circ\approx0.0174524064$ 。
一般而言，所有角的正弦比值都能被化約成銳角的，而超過 $45^\circ$ 的正弦可以用其餘角的餘弦，所以我們只要在 $0\leq x\leq \pi/4$ 的範圍裡計算正弦和餘弦的數值即可，而餘弦可以根據以下級數計算
$\begin{displaymath} \cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}-\cdots \end{displaymath}$

例如要計算 $\sin256^\circ$ 可以根據對稱性知道它等於 $-\sin76^\circ$ ，再轉成餘角，也就是 $-\cos14^\circ$ 換成弧度量便是 $-\cos(7/90)\pi$ 於是將 $x=(7/90)\pi$ 代入上式，計算前四項就得到 $10^{-10}$ 精確度的估計值。
多項式在數學中有其自身的旨趣，研究高次多項式的性質，具有數學內部的意義和需求。但是對大多數的數學「使用者」而言，多項式的價值在於其「以簡馭繁」的能力；這種能力，除了表現在資料的內插計算法 (例如回歸直線) 和描點曲線 (例如樣條函數) 之外，最成功的範例就是此處所舉的逼近能力。
讀者或可想像，在微積分之前，可能只有 8% 的人口能夠學到計算三角比值的程度。在微積分之後，透過上述那種無窮級數的公式，可能有 20% 的人口能夠從事計算。外插這個想像的數據，微積分使得更大量的人，可能是 30% 的人口，可以從事科學、工程或管理方面的創造性活動。這個情況，就好像武藝精湛的日本武士遇到了拿毛瑟槍的新兵。如此大量腦力的釋放，我認為是近三個世紀科技文明突飛猛進的基礎，也是歐洲人突然富強而橫掃整個世界的肇因。
當數學結合了資訊工具，包括電腦和網路，將會有更多的腦力被釋放出來，我猜可以達到 60% 的人口。但是，我們的教育內容、方法和制度，都還沒有跟上時代的腳步，這需要課程設計、教材教法和學習態度的全面改變。 98 年版的高中數學課程綱要 (草案)，就已經朝這個方向做了初步的邁進。

[ 回上層 ]

Back to the home page of Wei-Chang Shann.
Connect to the home page of Department of Mathematics, National Central University, Taiwan.

shann@math.ncu.edu.tw