經濟合作與發展組織 (OECD: Organisation for Economic Cooperation and Development) 為何要研議教育議題呢？簡單地說，因為經濟發展需要人才， 而人才需要教育來培養與訓練。 其國際性質促使她自 1997 年起執行跨國的學生評量計畫 (PISA: Programme for International Student Assessment)。 第一次的 PISA 2000 測驗著重於閱讀，第二次的 PISA 2003 則著重於數學， 第三次的 PISA 2006 著重於科學；而再下一次又會輪回閱讀。 跟 TIMSS 比起來，PISA 關心的年齡層稍微高一點，是 15 歲的青少年。 台灣並沒有參與前兩次的 PISA，但是參與了 PISA 2006。本文資料取自於 PISA 2003。
設計 PISA 國際測驗的團隊，想必瞭解「考試領導教學」的效果， 而我也認為他們顯示了如此的企圖心。在他們的 PISA 2003 報告中， 並非只是闡明命題內容、評分定義與統計程序，並且陳述測驗結果而已； 他們也闡述自己的教育理念，並在這份理念的哲學方針之下設計測驗。 例如，所謂「素養」一詞來自英文的 literacy，字面的意義只是「讀與寫的能力」； 而 PISA 定義「數學素養」為：
當面臨關於數量、形體、關係與不確定性等數學觀念的狀況， 運用知識與技能而提出、解決或解釋問題的時候，能夠有效地分析、推論和溝通。而 PISA 希望能夠評量「素養」。 我興味盎然地發現，OECD 這個以經濟學者、銀行家和企業家為班底的國際經濟組織， 做起教育的時候，確實讓人嗅到不同的氣息；簡單地說，他們顯得更實際。
我很高興看到 PISA 的理念中出現了我們正在綢繆的關鍵詞：溝通。 既然如此，正好透過他們的報告，特別是實際的測驗題目與評分標準， 看看這批務實的人，怎樣在PISA測驗中落實數學溝通的定義與評量。
PISA 將以數學方法解決問題的程序稱為「數學化」(mathematisation)。 數學化通常分為三個階段，我國的中學數學教師也都知之甚詳。
- 第一階段是瞭解狀況並設計數學模型， 例如設定未知數和寫出方程式之類的國中生功課。
- 第二階段是單純的數學，包括了計算與演繹，在數學內部就數學模型而推論； 這也是在數學課堂中投注最多時間與心力的部分。
- 第三階段是解讀數學推論的結果，國中教師通常稱這個步驟為「寫出答案」。
PISA 並不關心在數學化前端與中段的溝通問題， 他們著眼數學溝通的角色於整個數學化過程的後端， 這包括將數學計算或推論的結果轉譯成可以用來解決原本問題的程序或方法， 也包括解釋或辯證 (justification) 這份結果； 終極的辯證就是證明 (proof)。或許可以這樣解釋： 如果問題已經用數學形式或清楚的情境描述寫出來， 則「了解題意」這類前端的過程， 需要的是一般的閱讀能力與數學本身的訓練 (例如知道什麼叫做「偶數」，什麼是「和」)； 而中段過程裡的數學計算與演繹， 則屬於數學能力本身的訓練 (例如把條列的計算寫得正確而清楚)。 這兩者都可以附會地認為有數學溝通的成分， 但是 PISA 更關心在「解決問題」的最後階段所需要的數學溝通能力：轉譯與解釋。
既然 PISA 把數學溝通放在數學化的後端，顯示他們認為數學溝通能力的發展， 晚於基本計算能力與處理例行問題的能力發展。 這反映在 PISA 的評分標準裡。PISA 以六個等第評量學生的能力，愈高愈強。 前兩個等第根本不列溝通能力，從第三等第起才開始評判其溝通能力。 從第三等第：能夠簡短地報告其結果與推理過程，漸次提高到第六等第： 能夠精確表達其推理及省思過程，並能解釋數學結果針對原本問題的適用性。
四種數學主題 (見第二段) 各自有其能力分佈，
但是差不多有 5% 的學生達到最高等第，而總有略高於半數的學生達到第三等第。
換句話說，幾乎半數的受測 (15歲) 學生屬於相當基礎的前兩個等第
(甚至於不到第一等第)，這些人被認為還沒有發展數學溝通能力。
台灣的情況想像中應該比國際平均要好一些，
例如名列前茅的芬蘭、荷蘭、韓國與港澳地區，
經常有 10% 以上的學生達到第六等第。
以下我列舉幾個 PISA 的題目和評量標準，作為具體的範例。 一個數量主題的題組說：新加坡的美琳要到南非三個月， 她需要兌換新幣 (SGD) 與南非幣 (ZAR)。 當她出發的時候 1SGD=4.2ZAR，她兌換 3,000 新幣，問拿到多少 ZAR？ 這是第一等第的問題。 當她回來的時候，要換回剩下的 3,900ZAR，但匯率變成 1SGD=4.0ZAR， 問她能換回多少新幣？這卻是第二等第的問題。 這三個月的匯率從 4.2ZAR 變成 4.0ZAR，使得美琳獲益還是損失？ 書寫回答並需說明理由。這就是一個明顯的數學溝通測驗了，它列為第四等第。
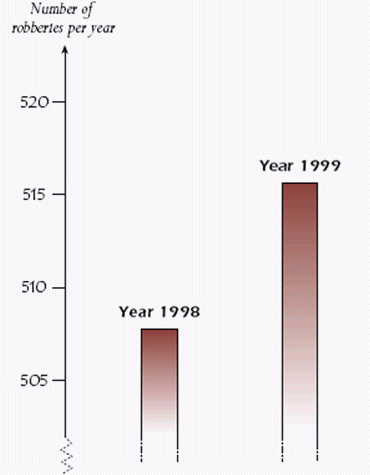
另一個屬於不確定性主題的題目：某電視播報員展示右側圖表， 並說『這張圖顯示 1998 至 1999 年間的搶劫犯罪數量暴增』。 請問播報員的說法是否為這張圖的合理解讀？ 如果學生能夠轉換成比例觀念，或者辯論是否暴增要看更多年的數據來判斷趨勢， 以指出播報員的不合理，則被認為具備第六等第的數學能力。 如果不能採用相對增加率的數學語言，而僅在絕對數值上反駁 (只在五百多件當中增加了八件左右，並不算「暴增」) 則被列為第四等第。
下面這個不確定性的問題則顯示 PISA 對第五等第的想法。
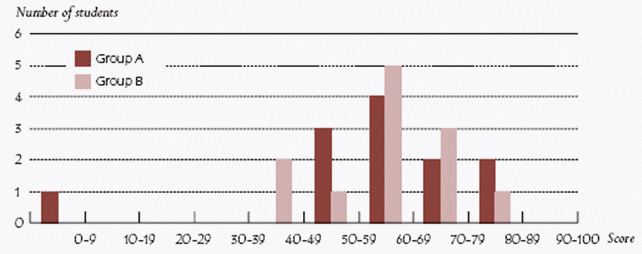
以下圖表顯示 A、B 兩組學生的測驗成績，50 分為通過測驗的門檻。
因為 A 組平均 62.0 分而 B 組平均 64.5 分，老師說 B 組表現較優。
如果妳是 A 組學生，該怎樣辯駁，說明其實 A 組較優？
如果學生能夠指出 A 組有一筆偏離 (outlier) 資料，
或者說 A 組通過測驗的人數比較多，則被評定為第五等第的數學能力。
