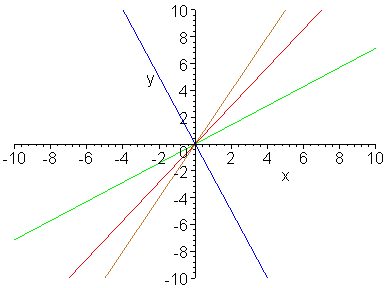
線型函數的函數曲線就是一條直線。它的基本形式是
就如同我們所熟悉的,函數也經常寫成
如果 a = 0 則線型函數就退化成常數函數 (constant function),
它的圖形就變成一條水平線 (平行於 x 軸的直線)。
否則,
參數 a 是線型函數的 斜率 (slope)。
當斜率是 0 的時候,圖形是水平線。
當斜率為正數時,直線向右傾,這個函數 漸增 (increasing)。
當斜率為負數時,直線向左傾,這個函數 漸減 (decreasing)。
斜率的絕對值越大,直線就越「陡」。
但是線型函數的圖形不能陡到變成垂直線 (垂直於 x 軸的直線),
因為,根據函數的定義,垂直線根本就不是一個函數曲線。
以下兩個動畫,分別示意 a (斜率) 和 b (y 截點)
對於函數圖形的影響。
| y = x + b, b = -8 .. 8 |
|---|
|
| y = a*x, a = 0 .. -2 | y = a*x, a = 0 .. 2 |
|---|---|
| 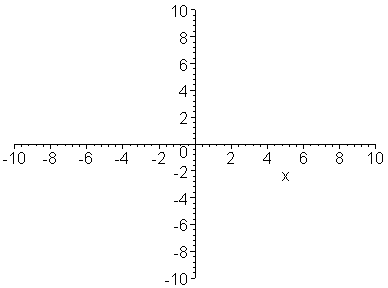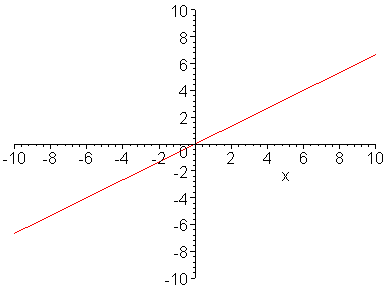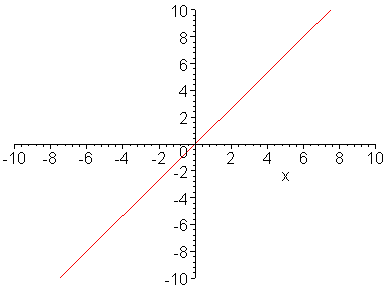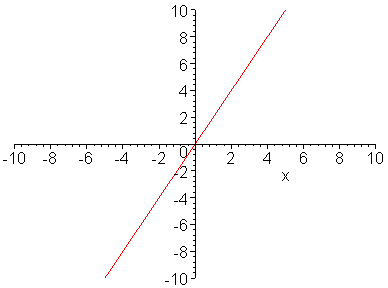
|
定義函數
線型函數從任何一點 x1 到它右邊另一點
x2 的變化率都是一樣的,都是
同學們可能會在線性代數這門課裡面學到所謂線性映射。 線性映射和線性函數是不太一樣的。 簡單地說,通過原點 (也就是 b = 0) 的線型函數, 是一維的線性映射。 當 b 不是 0 的時候,線型函數不是線性映射。