指數函數
指數函數的基本型態是
其中 k 和 a 是兩個 (實數) 常數。
k 稱為係數而 a 稱為 底數 (mantissa)。
底數 a 必須是正數
(當然 a = 0 也沒什麼不對,只是我們不考慮這個無聊的狀況)。
以下舉一些指數函數的例子。
- 經濟的例子
所謂「成長率」是比前期增加的比率。
例如今年的經濟比去年成長了 3% 的意思是,
今年的經濟規模是去年的 1.03 倍。
相反地,如果今年的經濟比去年衰退了 3%,或者說成長了 -3% (負成長),
意思是今年的經濟規模是去年的 0.97 倍。
如果今後十年每年都維持 3% 的成長,則令今年的經濟規模是 P0,
t 是從今年算起的年數 (今年是 t = 0,
明年是 t = 1,依此類推),則每年的經濟規模是一個 t 的指數函數:
反之,如果今後十年的經濟規模都維持每年 3% 的負成長,則
由此或可瞭解,何以底數總是正數。
- 生物的例子
以下是一個頗為簡化的生物增長模型:當食物與空間無限充裕且沒有競爭的時候
(所以顯然在台灣不適用),一個生物族群的數量可以維持固定的成長率。
例如 1980--1986 年間的墨西哥人口數
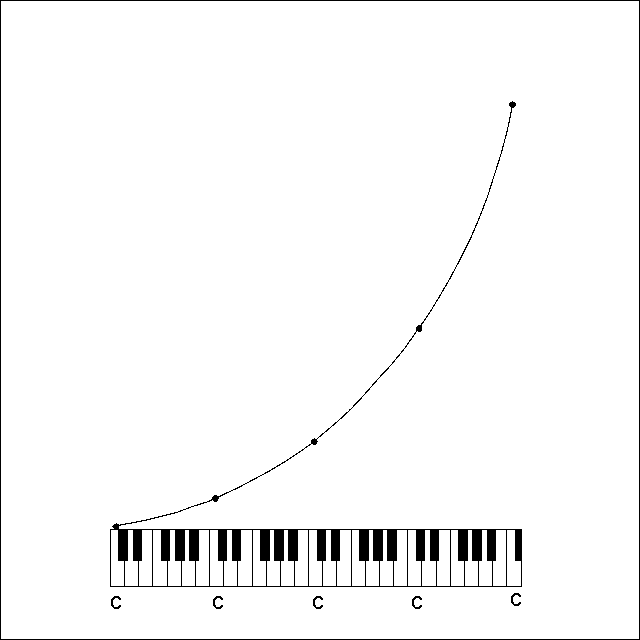
- 音樂的例子
我們耳朵聽起來相差八度音階的兩個音,其頻率其實是相差一倍:
若一個音的頻率是 a Hz (每秒振動次數),
則 2a 頻率的音,聽起來高了八度。
所以,如果鋼琴上中央 C 的 Do 頻率是 256 Hz (真實情況差不多如此),
則低八度的 Do 頻率是 128 Hz,而高八度的 Do 頻率是 512 Hz。
以下是鋼琴鍵盤與頻率的函數關係示意圖,橫軸是鍵盤,縱軸是頻率。
- 物理的例子
放射性物質有所謂的 半衰期 (half-life)。
所謂半衰期就是衰退到原來的量的一半所需要的時間。
例如碳十四的半衰期是 5730 年,則物質中碳十四的含量
是時間 t (以年為單位) 的指數函數:
其中
是原來的碳十四含量,它是個常數。
考古學家以今天活著的爬蟲類 (或鳥類) 體內的碳十四含量當作
,
並以恐龍化石中測得的碳十四含量代入上式,
來估計恐龍的年代。
因為 a 0 = 1,所以指數函數總是符合
。
在這篇教材裡,我們都只考慮 k > 0 的情形。
所以指數函數
恆為正數。
如果 a > 1,則當 x 越來越大,
也越來越大。但是當 x 越來越小,
就越來越靠近零。記做
如果 0 < a < 1 (k 還是 > 0),
這是負成長或衰退的情況。
此時
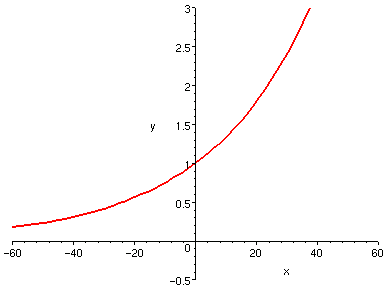
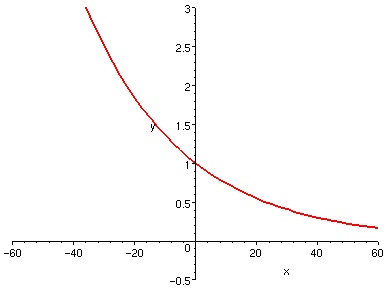
還是恆正,只是越來越小:看以下兩個示範圖形:
| y = (1.03)^x
| y = (0.97)^x
|
|---|
| 
|
比較指數函數和冪函數 (只比正數的部分)。簡單地說,
指數函數永遠跑得比冪函數快
意思是說,如果 a > 1 和 p > 0,
只要 x 夠大,
總是會超過
。
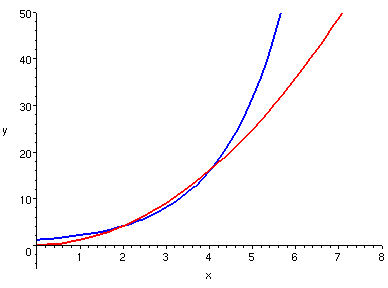
看以下兩個例子。
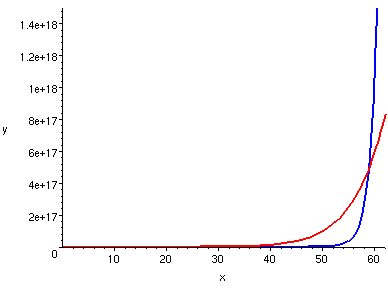
| y = x^2, y = 2^x
| y = x^10, y = 2^x
|
|---|
| 
|
我們看到,藍隊總是獲得最後的勝利(如果比賽得夠久的話)。
所以說,雖然當 a > 1 和 p > 0 的時候
但是在趨向無窮大的速度上,指數函數終究會超過冪函數,
不論 p 比 a 大了多少。
反過來,如果 0 < a < 1 和 p < 0,
還是指數函數跑得快。
意思是說,只要 x 夠大,
總是會比
更接近零。
看以下兩個例子。
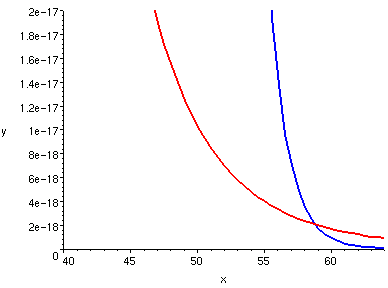
| y = 1/x^2, y = (1/2)^x
| y = 1/x^10, y = (1/2)^x
|
|---|
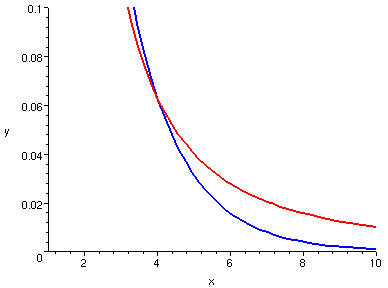
| 
|
所以說,雖然當 0 < a < 1 和 p < 0 的時候
但是在趨近於零的速度上,指數函數終究會超過冪函數。
習題
- 題目
- 估計鋼琴上最高音的頻率大約是多少?
- 估計鋼琴上最低音的頻率大約是多少?
- 人類耳朵據實驗只能聽到 22,000 Hz 以下的聲波。
請問,從鋼琴上中央 C 的 Do 算起,一共能聽到幾個八度音階?
- 鐳 (266) 的半衰期是 1620 年,請問任何一個含鐳物質放置 500 年後,
它的鐳含量是現在的百分之多少?[HH]
- 文書編輯的經驗是,每次對一本厚書做校對,可以訂正 80% 的錯誤。
如果一本書的初稿有八十萬字(紅樓夢就差不多有這麼多字),
假設該作者大約每三千字就會犯一個錯誤。
請問要校對幾遍可以假設沒有錯誤了?
- 假設某種抗生素在人體內每小時會被代謝排泄掉 40%。
每次注入的劑量是 250 毫克。如果在療程中要保持劑量在 10 毫克以上,
請問每隔多久就應該注入一次?
- 猜想
說明為什麼?
- 猜想
說明為什麼?
Created: Oct 16, 1996