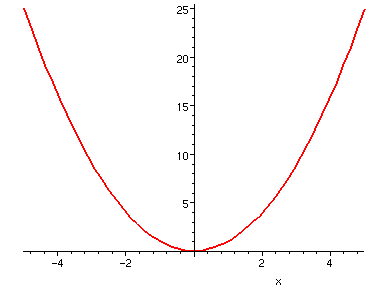
| y = x^2 |
|---|
|
如果函數
以類似的定義,我們說函數漸減 (decreasing) 或不遞增 (non-increasing), 或者嚴格漸減 (strictly decreasing)。 因為非常類似,就不再贅述了。
例如 x 2 在
我們看到,當函數漸減的時候,曲線下降;漸增時,曲線上升。
注意,我們一律順著自變量座標軸的方向(通常是從左到右)解讀函數曲線。
y = x^2

當底數 a > 1 的時候,指數函數
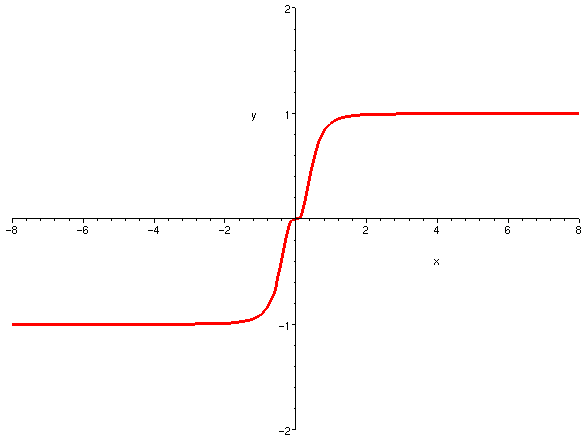
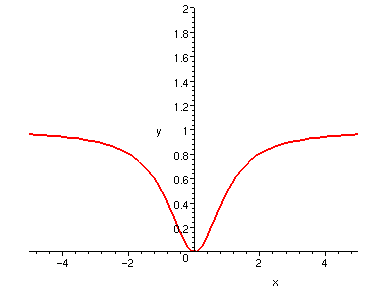
一個函數如果不停地嚴格漸增,未必會趨於無窮大;
因為有可能有水平漸近線。如下圖。
|
一個函數若是漸增或者漸減,統稱為單調函數 (monotonic function)。
例如線性函數、指數函數與對數函數,都是單調函數。
一個 n 階多項式的曲線,至多有 n - 1 次轉折,
也就至多可以將實數分為 n 段,在每一段內都是單調的。
注意,是「至多」,所以 n 階多項式還是有可能是單調函數。
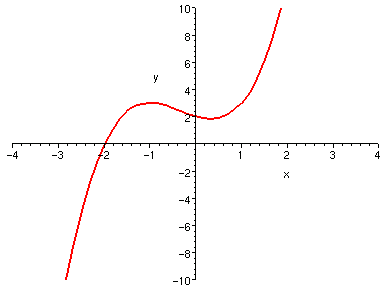
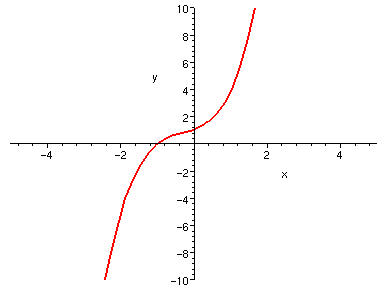
參考以下兩個範例,它們都是三階多項式,一個轉折兩次
(漸增、漸減、漸增),一個沒有轉折 (單調)。
| y = x^3 + x^2 - x + 2 | y = x^3 + x^2 + x + 1 |
|---|---|
| 
|
這一節提到的形容詞:漸增、嚴格漸增、漸減、嚴格漸減、不遞增、不遞減、單調, 都不是統一的專有詞彙。其他作者可能用了同樣的詞卻給定不同的意義。 讀者需要小心檢查這些詞在不同書本裡面的定義。
|

|