函數的奇偶性質

如果函數在整個實數上有意義，也就是說它的定義域是而且其曲線對稱於垂直軸 (y 軸)，我們稱為 偶函數 (even function)。偶函數都符合以下性質：

的函數圖形，就是把

的圖形沿著 y 軸鏡射過去 (左右翻轉)。如下圖的示範：

f(x), f(-x)

所以，左右翻轉之後圖形不變的函數曲線，就是偶函數的曲線。例如 x ² 就是一個偶函數：

y = x^2

如果函數的定義域是而且其曲線奇對稱於垂直軸 (y 軸)，意思是說，把 y 軸右邊的曲線先鏡射到左邊 (對稱)，再以 x 軸做鏡射，就等於 y 軸左邊的曲線。這種情形，我們也會說的圖形對稱於原點。這樣的話，我們稱為 奇函數 (odd function)。奇函數都符合以下性質：

的函數圖形，就是把

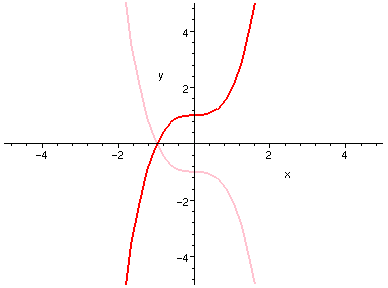
的圖形沿著 x 軸鏡射過去 (上下翻轉)。如下圖的示範：

f(x), -f(x)

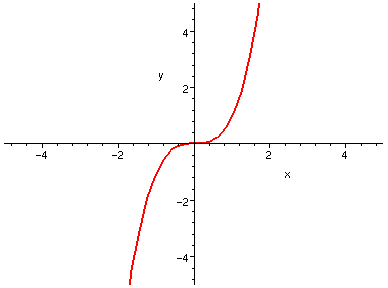
所以，上下翻轉之後的圖形與左右翻轉之後的圖形相同者，就是奇函數的曲線。例如 x ³ 就是一個奇函數：

y = x^3

除了常數函數之外，偶函數絕不可能是單調函數。但是奇函數卻可能是單調的，例如 y = x 或 y = x ³ 都是。指數與對數函數都不是偶函數 (除了無聊的情況外) 也不是奇函數。