其實,函數的上下平移,就是函數與常數函數相加。
將兩個函數相加,
其實就是把他們的值加起來,沒什麼好說的。
以後會經常看到函數的和。
要提醒讀者的是,函數的和,有時候會產生令人驚奇的結果。
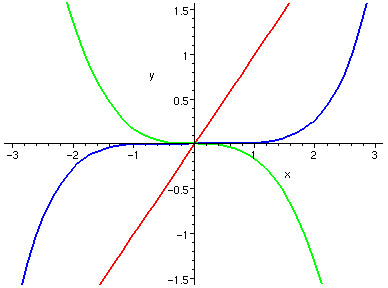
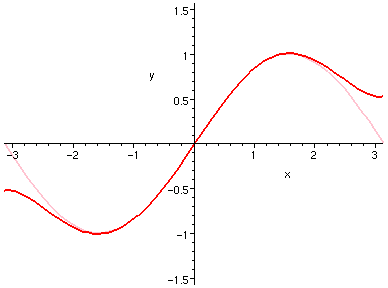
以下左邊是三個冪函數的圖形,把它們加在一起,卻出現又邊那個圖形。
而又邊那個圖形,幾乎是正弦函數的曲線!
| y=x, z=-x^3/6, w=x^5/120, | y+z+w, sin(x), |
|---|---|

| 
|
既然談了相加,就包含了相減 (先乘上 -1 再相加),因此不再贅述。
其實,將函數拉高,就是函數與常數函數相乘。
兩個函數相乘,在一個靠近 1 的時候,函數積靠近另一個函數的曲線;
在一個有根的時候,函數積也有根。
實際應用中,最常見的函數相乘,就是「阻尼震盪」:
一邊震盪、一邊縮小震幅,最後趨於不震動。
就好像汽車駛過路面高突之後,避震器不好的汽車,會上下震盪久一點;
避震器比較好的汽車,可能只會讓乘客感覺一兩次的震盪。
參考以下圖示。
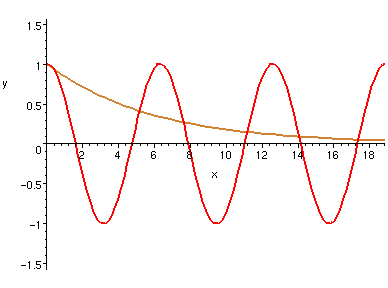
為了讓讀者看清楚函數相乘的效果,我們故意展示一個避震器不良的「阻尼震盪」效果。
左圖是兩個函數,一個代表震盪 (cos(x)),另一個代表阻尼 (damping) (2^(-x/4))。
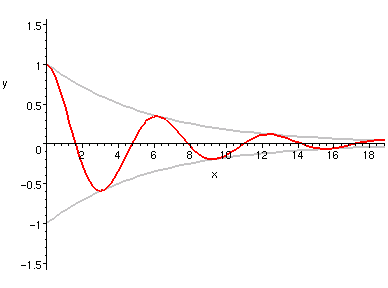
右圖是它們相乘的結果。我把阻尼函數用灰色再畫兩遍,
使大家看出來,阻尼函數好像把震盪函數「上下夾住」的樣子。
| y = cos(x), z = 2^(-x/4), | y*z, z, -z, |
|---|---|
| 
|
既然談了相乘,就應該談相除。 做為分母的函數,如果沒有根,那麼情形就與相乘是一樣的: 相除就等於與倒數相乘。 如果分母函數有根,那就要討論漸近線了。我們不再深入去討論。