函數的拉高與上下平移
上下平移
將函數
拉高
將函數
乘上一個常數 a ,也就是
。
我們不考慮 a = 0 的無聊狀況。
而且,我們已經知道,如果 a < 0 就是先將曲線上下翻轉,
再乘上 |a| 的意思。
所以,我們現在只討論 a > 0 的情況。
其效果就是將原來的曲線拉高 (raise) a 倍
(如果 a < 1 就是負的拉高,變成壓扁)。
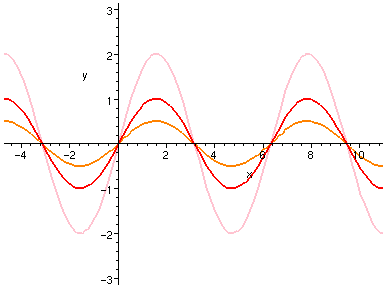
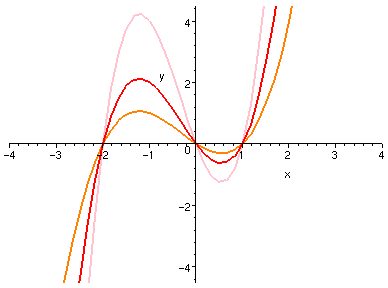
這是很容易瞭解的,如下圖所示範。
| f(x),
2*f(x),
f(x)/2,
| f(x),
2*f(x),
f(x)/2,
|
|---|
| 
|
被拉高的曲線根的位置沒有改變,所以看起來「寬度」沒變,
因此就顯得「瘦高」或「矮胖」了。
顯然函數的最大值與最小值 (如果有的話) 也乘了 a。
習題
- 請問 3*sin(x) 的最大值、最小值分別是多少?
- 請問 3*cos(x) + 3 的最大值、最小值分別是多少?
- 請問 tan(x) - 1 的根有哪些?(函數曲線與 x 軸交點,簡稱為「根」)
Created: Jul 26, 2001


