![[Fig 26]](../../calcware/figs/fig26.gif)
直角三角形三個邊的兩兩比值,就定義了六種三角函數。 根據直角三角形的幾何性質,這六個函數其實都可以從一個函數導出來。 因此,之所以要說六個,而不是一個,只是為了應用上的方便。 我們就從那最基礎的一個開始:正弦 函數 (sine):
當 x 是一個銳角的角度時,sin x 有簡單的幾何意義,如下: 考慮一個以 x 為一夾角的直角三角形, 則 sin x 就是 x 之 (對邊 : 斜邊) 的比值。 因為所有有一個角是 x 的直角三角形都相似,而且我們只關心邊長之間的比值, 所以不必理會各邊的長度。 因此,我們可以隨我們的方便,規定三邊裡其中一邊的邊長 (另外兩邊就自動決定了)。例如,規定斜邊長是 1,參照下圖
![[Fig 26]](../../calcware/figs/fig26.gif)
角 x 的度量單位,至少有兩種:所謂的角度和弧度。 角度是小學生都知道的,一個圓周等分成 360 分,是為 360 度。 弧度應該是在高中學的,是半徑為 1 的 單位圓 (unit circle) 上, 圓心角為 x 所對的弧長。 因此,同一個角 x,以角度為單位,其數值介於 0 與 360 之間; 以弧度為單位,其數值介於 0 與
高等數學一向採用弧度單位來測量角。 為什麼選擇採用弧度而不用角度? 答案與微積分有關,我們稍後再解釋。
至於 sin x 的值呢?根據畢氏定理, 我們知道幾個特殊角的正弦值。 例如
如果角度不是銳角,而是介於
sin (2.5)
sin (1/2)

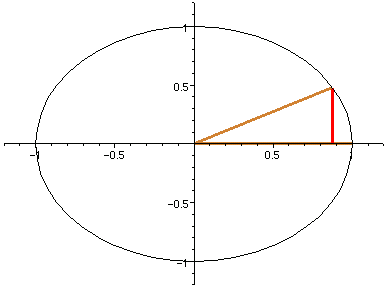
sin (4)
sin (2*Pi-1)
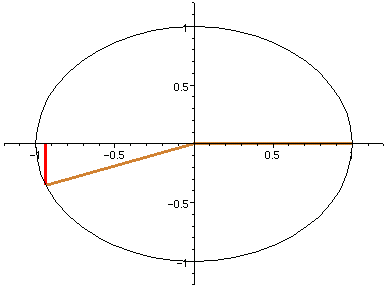
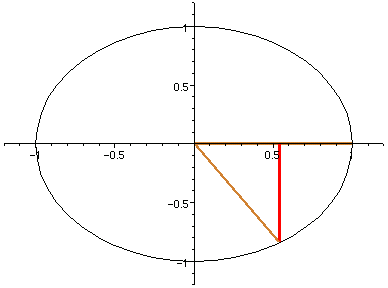
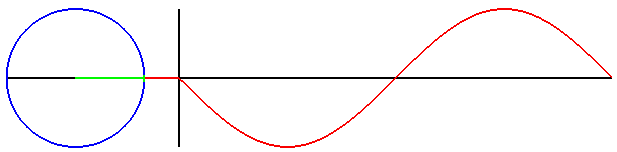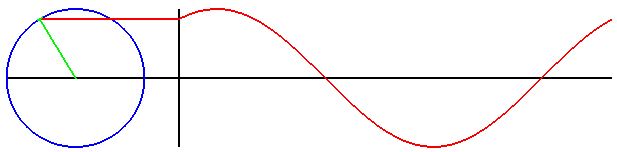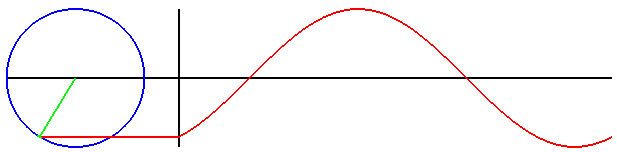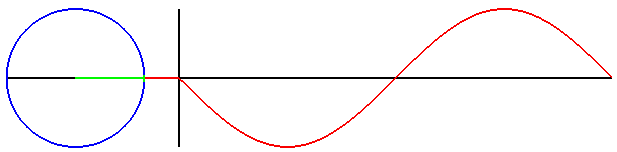
另一種瞭解正弦函數的方式,是想像一個在單位圓上以逆時針方向等角速度旋轉的點 P。
則點 P 的 y 座標與時間的關係,就是正弦函數。參照以下動畫。
以下是
| sin(x), x=0..Pi, y=-Pi..Pi |
|---|

|
當 x < 0 或是 x > 2*Pi, 我們可以定義「廣義角」。就好像圓周上的點,轉了一圈又一圈, 但是都還是在同一個圓周上。 對於廣義角 x,我們總可以找到唯一的一個整數 n, 使得
| sin(x), x=-2*Pi .. 4*Pi |
|---|
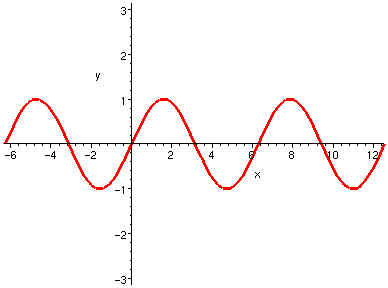
|
讀者不難觀察,正弦函數是奇函數。也就是說,
另 x 是一個銳角,再度考慮一個某一角為 x 的直角三角形。
則 x 的餘弦 (cosine) 就是 x 之 (鄰邊 : 斜邊) 的比值。記做
如果 x 不是銳角,甚至是廣義角,都用同一個 (上述) 公式來計算。
由此可見,餘弦值其實可以由正弦值求得。同樣地,
而以下是 cos x 的曲線圖形。
可以看得出來,它和正弦函數「看起來好像」。
注意 sin(0)=0 而 cos(0)=1。
cos(x), x=-2*Pi .. 4*Pi
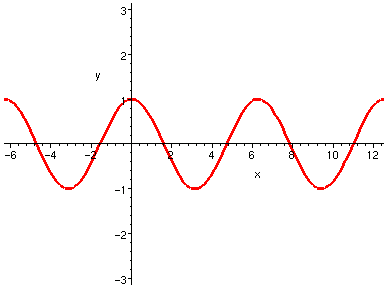
讀者不難觀察,餘弦函數是偶函數。也就是說,
還是一樣,先考慮 x 是一個銳角,我們定義它的幾何意義,
再推導計算公式,並依照該公式處理非銳角的 x。
| 正切 | tangent | (對邊 : 鄰邊) 的比值 |
| 餘切 | cotangent
| (鄰邊 : 對邊 ) 的比值
|
| 正割 | secant
| (斜邊 : 鄰邊) 的比值
|
| 餘割 | cosecant
| (斜邊 : 對邊) 的比值
|
| |
|---|
過去的中學生都學過一個六角形示意圖, 來幫助我們記憶這六個三角函數之間的基本關係。
![[Fig 27]](../../calcware/figs/fig27.gif)
除了上述的基本關係,請各位同學複習幾個常用的等式。 至少包括以下四組:
在這六個三角函數中,我們比較關心正弦、餘弦、正切三個。
因為直角的餘弦是 0,亦即
由於 tan x 的分母是 cos x,
所以 tan x 在這些點上沒有意義。
換句話說,正切函數的定義域是
以下是正切函數的曲線圖形:
tan(x), x=-2*Pi .. 4*Pi
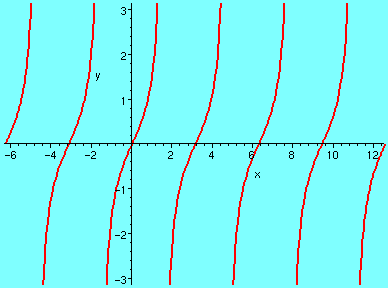
習題