函數的脹縮平移

脹縮 (dilation)

令 a 是一個正數，則函數 的圖形與原來的函數 一樣高，但是「寬度」改變了。我們先想一個簡單的例子。 如果 原來在 x = -1 和 x = 1 處有根， 那麼 的根就發生在 2x = -1 和 2x = 1 處， 也就是 x = -1/2 和 x = 1/2 處。 是不是看起來函數「縮窄」了？ 另一方面， 的根就發生在 x /2 = -1 和 x /2 = 1 處， 也就是 x = -2 和 x = 2 處。 是不是看起來函數「脹胖」了？參考以下圖示。
f(x),   f(2*x) f(x),   f(x/2)
   

所以我們結論，如果 0 < a < 1，則 的圖形比原來的 脹胖了 1 / a 倍。如果 a > 1，則 的圖形比原來的 縮窄了 a 倍。

如果 a 是個負數，則相當於先左右翻轉 (對 y 軸鏡射)， 再根據 | a | 來脹縮。

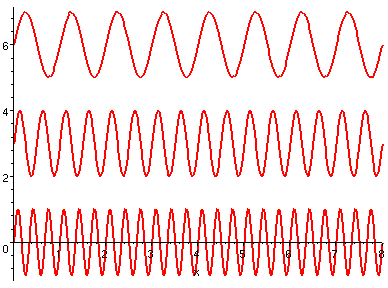
三角函數在經過脹縮之後，週期改變了。例如 原本在 [0, ] 區間內是一個週期，那麼 就是在 這個範圍內完成一個週期。也就是 完成一段週期。因此， 成為一個 1-週期函數，它的頻率是 1。而 就會成為一個 (1/2)-週期函數，它的頻率是 2。 以下圖片中，我們顯示頻率為 1, 2, 3 的正弦函數。
 

平移 (translation)

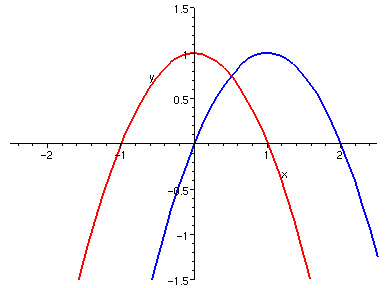
如果 s 是一個正數，則 的函數圖形，是原來 的圖形向右 (x 軸的正方向) 平移 s 個單位。 如果 s 是負數，則代表向反方向平移，也就是向左平移。 它們的圖形外觀完全沒變，只是位置改變了。 我們先想一個簡單的例子。如果 原來在 x = -1 和 x = 1 處有根， 那麼 的根就發生在 x - 1 = -1 和 x - 1 = 1 處， 也就是 x = 0 和 x = 2 處。 是不是看起來函數「向右平移」了？ 另一方面， 的根就發生在 x + 2 = -1 和 x + 2 = 1 處， 也就是 x = -3 和 x = -1 處。 是不是看起來函數「向左」了？參考以下圖示。
f(x),   f(x-1) f(x),   f(x+2)
   

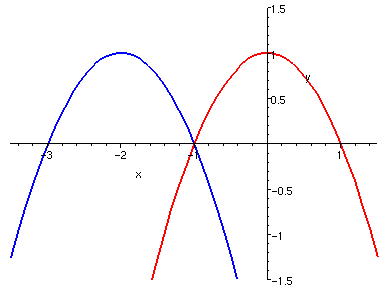
很明顯地， 就是將 曲線先左右翻轉之後，再平移。 但是，依照前面所展示的要領，讀者不難發現，此時平移的方向原則，要相反了： 當 s > 0 時，向左平移；當 s < 0 時，向右平移。 例如我們已經知道



也就是說，先將正弦圖形左右翻轉，再向右平移 就得到餘弦圖形。見以下圖示。
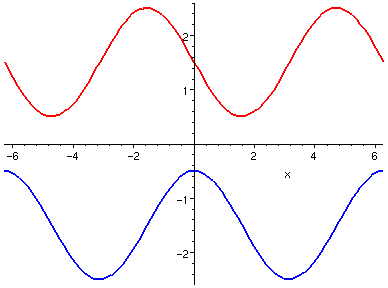
sin(x) + 1.5,   sin(-x) - 1.5 sin(-x) + 1.5,   sin(Pi/2 - x) - 1.5
   

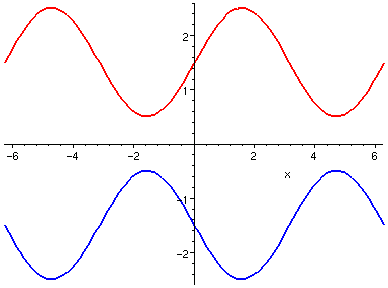
三角函數的平移量，稱為 相位差 (phase difference)。例如 的相位差就是 (落後) 。 如果想像 x (廣義角) 是圓周上的點， 想像所謂「正常相位」就是從 0 度開始旋轉。 那麼所謂相位差，就是說它落後或領先了「正常相位」多少角度的意思。 以下動畫，展示落後 的正弦波與「標準」正弦波的比較。

因為三角函數的週期性，所以可以只考慮介於 0 和週期之間的相位差。 因為只要相位差等於週期，就好像圓周上落後整整一圈的點，其實看起來並沒有落後。 例如以下動畫，就顯示了


的曲線，而讓 從 0 變化到 。
sin(x-theta), theta=0...
 

三角函數的脹縮平移

至此，我們瞭解，三角函數的脹縮，就是改變它的週期 (也就是改變頻率)。 三角函數的平移，就是決定它的相位差。 而三角函數加上一個常數，是決定它的平均值 (最大值與最小值之平均)； 三角函數乘上一個常數，是改變它的振幅。 自然界中，諸如日照之長短、潮汐之漲落、月亮之盈虧， 基本上都是週期性的變化。 只要是週期性的變化，就可以設法用正弦函數描述出來： 只要決定了週期現象的：週期 (T)、相位差、平均 (M)、振幅 (A) 就可以寫出週期函數了。其一般形式是



例如，令 是某地在每年第 x 日的「白天時數」。 所謂白天時數是指當天日出到日落之間的小時數，與當天實際的天氣陰晴無關。 而 x 的單位是日，從每年的一月一日開始算起， 而忽略潤年 (也就是每年假設 365 日)。 從地理常識，我們知道 與所在地的經度無關，與緯度有關 (如果忽略地形所造成的影響)。 而不論緯度如何，每年的平均白天時數都一樣，應該是一天的一半：12 小時。 所以 M = 12。而 A 就應該與緯度有關， 在赤道上，日照時數在一年中的差異很小，越往兩極就差異越大， 南極與北極甚至有永晝和永夜。以北級而言，其 的最大值是 24 (永晝) 而最小值是 0 (永夜)，因此對應 A = 12。 在台灣，A 大約是 2.5；也就是夏天最長的一日， 大約有 14.5 小時的白天。 的週期顯然是 365，而 。 到目前為止，我們知道，對台灣而言，大約



該怎麼決定 呢？我們知道，在春分那一天，白天與夜晚等長 (各 12 小時)， 所以那時候的正弦函數值應該是 0。春分是三月二十一日，對應 x = 80。 我們令


解得 。 或者，我們可以乾脆就寫


習題

  1. 題目
  2. 題目
  3. 如果 在 [0,1] 區間內的函數值為正數，在其他地方的函數值為 0。 請問 在哪個區間內的函數值為正數？
  4. 如果 在 [0,1] 區間內的函數值為正數，在其他地方的函數值為 0。 請問 在哪個區間內的函數值為正數？
  5. 如果 在 [0,1] 區間內的函數值為正數，在其他地方的函數值為 0。 請問 在哪個區間內的函數值為正數？
  6. 如果 在 [0,1] 區間內的函數值為正數，在其他地方的函數值為 0。 請問 在哪個區間內的函數值為正數？
  7. 請問 的週期是多少？頻率是多少？
  8. 請問 的週期是多少？頻率是多少？
  9. 令 n 是一個正整數，請問 的頻率是多少？
  10. 請問 的週期是多少？
  11. 請問 的週期是多少？
  12. 根據和差公式，帶有相位差的正弦函數，可以轉換為沒有相位差的正弦和餘弦函數。 一般而言：


    請問


Created: Jul 30, 2001
Last Revised: Jul 30, 2001
© Copyright 2001 Wei-Chang Shann 單維彰