從圖形認識微分
在
現在,我們以
和 x0 = 1 為例,
在以
這個點為中心,
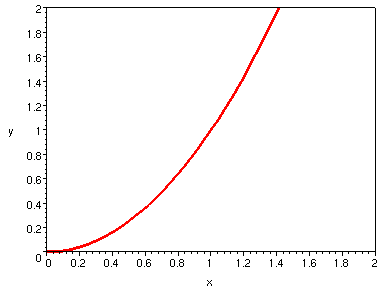
為邊長的正方形範圍內觀看
的曲線。
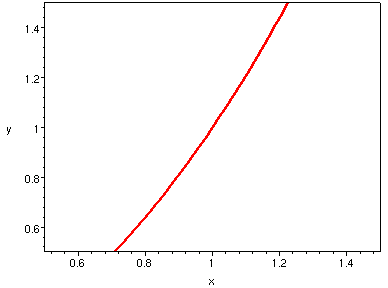
| h = 1 | h = 1/2
|
|---|
| 
|
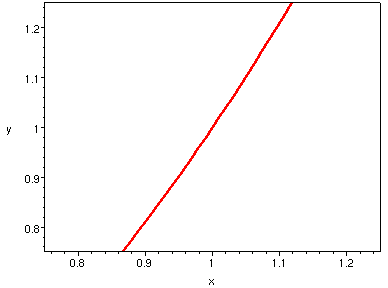
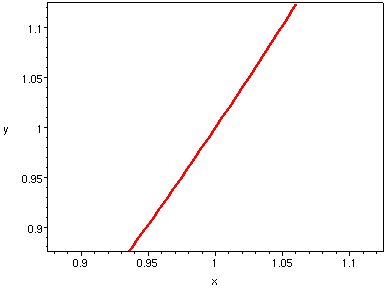
| h = 1/4 | h = 1/8
|
|---|
| 
|
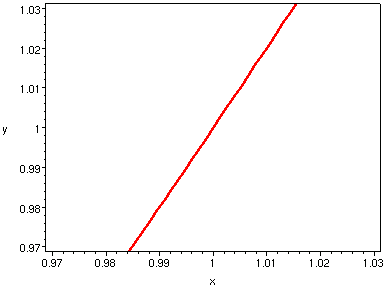
| h = 1/16 | h = 1/32
|
|---|
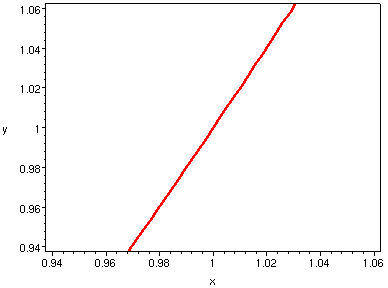
| 
|
如果我們知道函數
在 x0 附近幾乎是一條直線,而此直線的斜率是 m。
則因為此直線通過
這一點,所以根據「點斜式」我們可以寫出這條直線的線性函數方程式
利用這個資訊,我們可以估計
在 x0 附近的函數值。亦即,
只要
是個「很小」的數,
舉個例子,如果我們知道
在 x0 = 1 附近幾乎是一條斜率為 2 的直線,則
這個估計值和真正的值 0.8836 之間只有千分之三的誤差。
習題
- 如果我們知道
在 x = 1 附近幾乎是一條直線,而此直線的斜率是 0.5。
請問,根據這個資訊,您可以估計
大約是多少?它的五位有效數字「真正數值」是 1.0296。
- 如果我們知道
在 x = 0 附近幾乎是一條直線,而此直線的斜率是 1。
請問,根據這個資訊,您可以估計
大約是多少?它的小數點下四位「真正數值」是 0.1197。
- 如果我們知道
在 x = 1 附近幾乎是一條直線,而此直線的斜率大約是 1.3863。
請問,根據這個資訊,您可以估計
大約是多少?它的小數點下四位「真正數值」是 1.8921。
Created: Apr 16, 1997










