什麼是積分？

如果在閉區間 [a, b] 內是一個正值的連續函數，則所謂在 [a, b] 內積分 (integrate) 就是求函數曲線在 [a, b] 範圍內與橫軸圍成的區域之面積 (area)。如下圖

積分的結果稱為積值 (integral)。為了簡便，我們經常就只是說：積分就是求曲線下的面積。以後我們也會這樣說。但是，我們必須要知道，這樣說得背後，有一些細節要注意：閉區間、連續函數、正值。

說到面積，我們都耳熟能詳。對面積的認識，可能已經屬於我們的直覺的一部分了。的確，每個人對面積都有直觀的認識。例如下面左圖中的兩個區域，每個人都看得出來，哪個面積比較大。但是，誰看得出來右圖中的兩個區域，哪個面積比較大嗎？

因此，單靠直覺是不夠的，我們需要數字。也就是說，我們所謂的面積，其實是跟隨著某個幾何性質的一個數字。在應用上，面對一個圖形的時候，我們需要一套明確的算法, 用以求知它的面積。

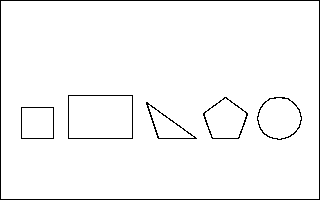
但是，回顧所有我們知道的計算面積公式，實在是少得可憐。基本上，我們其實只知道矩形面積的算法。這其實也是面積的定義。從矩形的面積，我們推導出三角形的面積，及至於多邊形的面積。如下圖所示。

圓的面積是一個奇特的例子，我們通常只是背公式，知道它是

至於它是怎麼來的？卻不甚了了。

既然我們只知道那麼少種類的面積計算公式，更徨論任意曲線下的面積呢？所以，當我們說，積分就是求曲線下面積時，我們只是在觀念上有所瞭解，其實並不知道到底該怎麼做。

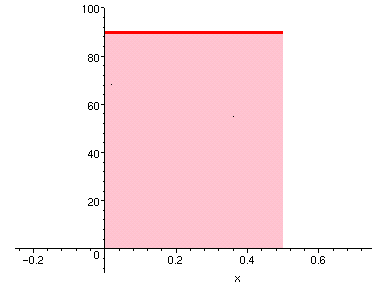
有何必要去求一個曲線下的面積呢？舉一個很簡單的例子。如果 y 代表一輛汽車以 km/hr 為單位的速率， x 代表以小時為單位的時間。則 y 與 x 的關係可以寫成一個函數。如果在時間開始計算的 30 分鐘內，汽車以定速 90 km/hr 行駛，則在 [0, 1/2] 區間內是常數函數 y = 90。在這段時間內，汽車總共行駛了 1/2 * 90 = 45 公里。這不就是在 [0, 1/2] 區間內的曲線下面積嗎？

但是，很少有汽車可以維持半小時的等速行駛 (特別是在台灣的市區或高速公路，除非速率是零)，所以一般而言

的曲線不是水平線。但不論如何，現在我們應該理解，如果

代表速率，則

的曲線下面積，就代表總共的位移量。

習題

如果函數中，自變量 x 代表時間 (以 hr 作單位)，應變量 y 代表馬達抽出的水量 (以 m^3/hr 作單位)。請問在 [0, 1] 內的積值代表什麼意義？
如果函數中，自變量 x 代表高速公路的里程碑 (以 km 作單位)，應變量 y 代表車流密度 (以輛/km 作單位)。請問在 [20, 60] 內的積值代表什麼意義？
如果函數中，自變量 x 代表從依天凌晨算起的時間 (以 hr 作單位)，應變量 y 代表消耗的電力 (以千瓦作單位)。請問在 [9, 17] 內的積值代表什麼意義？