sin(x)/x 當 x 趨近於 0 的極限是 1

考慮以下問題

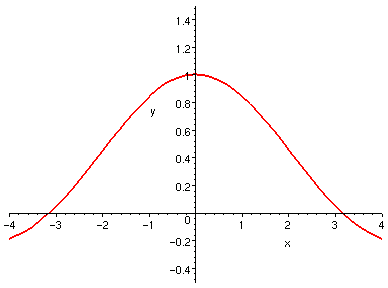
求極限的函數在 x = 0 處沒有定義。從圖形觀之，如下，

自數值觀之，如下 (因為這個函數顯然是偶函數，所以我們就不測驗 x < 0 的數值了)，

不論怎麼看，其極限都似乎是 1。但是，要怎麼「證明」呢？以下我們看一個古典的範例。

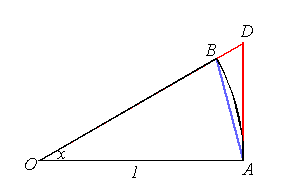
參照下圖

圖中的角 x 乃是以弧長為單位，扇形 OAB 的半徑是 1，因此弧線 AB 的長度是 x。 OB 射線與 OA 的垂直線相交於 D。很明顯地，

三角形 OAB 的面積 <= 扇形 OAB 的面積 <= 三角形 OAD 的面積.

由於 OB 的長度是 1，根據正弦的定義，三角形 OAB 的高是

。由於 OA 的長度是 1，根據正切的定義，三角形 OAD 的高也就是 AD 的長度，就是

。所以,

求極限的函數是偶函數，所以可以假定 x 為正數。 x 是要趨近於 0 的，所以它應該很小，於是可以假設

。則

。於是可得

或者

因為餘弦函數是連續函數，所以

而不等式的另一邊是常數函數。現在，引用夾擊定理，得證

這個漂亮的答案，必須以弧長當作角的測量單位，才能獲得。如果用角度，雖然此極限也會收斂，但是答案就比較醜了。

例一

我們曾經強調，

的極限型式，什麼答案都有可能，千萬不要亂猜。舉例來說，問

初學的讀者很容易就猜是 1，因為這個型式和前面的結果太像了。只要稍微做些計算，就知道答案可能是 2，如下。

正確的作法，是要利用變數變換湊出已知的極限：令

，則