積函數
令
在前面的定義當中,我們使用了 傀儡變數 (dummy variable) 的伎倆。
因為
和
都爭著要用 x 這個名字當作自變量,如果它們分別使用 x,
那就沒有問題。但是如果要寫在同一個式子裡面,那就可能造成語意混淆,
所以總有一個函數的自變量要換個名字。
我們把 f 的自變量改名字叫做 s。
但是,改個名字,絕對不會影響這個函數的本質。只是,例如,把
改成了
、
改成了
,
如此而已。聰明的讀者,一定是一看就明白了。
(還有,在座標平面上畫圖的時候,把橫軸的名字,從 x 改成 s。
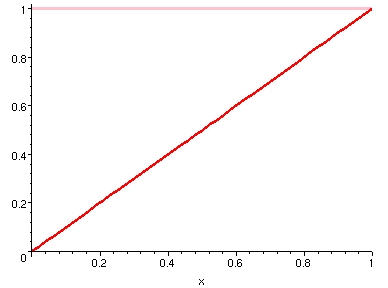
- 例一
-
令
,
在 [0, 1] 區間內考慮其積函數。則對任一個區間內的數 x,
在 [0, x] 內所圍成的區域是一個矩形,其面積就是 x,因此
。
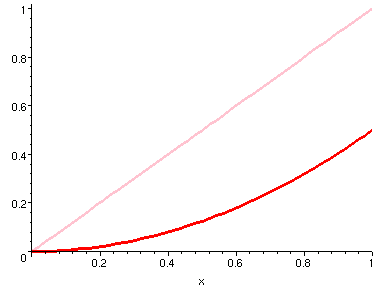
- 例二
-
令
,
在 [0, 1] 區間內考慮其積函數。則對任一個區間內的數 x,
在 [0, x] 內所圍成的區域是一個等腰直角三角形,
其面積就是
,
因此
。
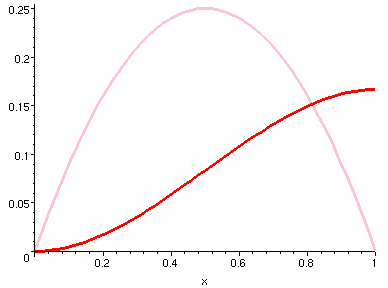
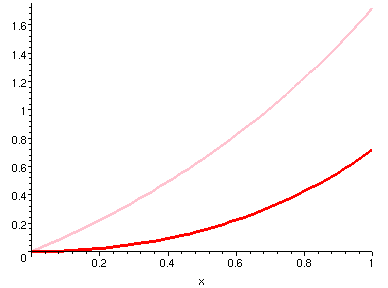
- 例三
-
我們在以下圖示中,展示四組函數與其積函數的對照曲線。
圖中紅色是粉紅色的積函數曲線。
前兩張就是例一和例二的圖。
從前面的例一和例二看來,讀者有沒有發現,原函數
和
之間,恰好都符合
這不是巧合,而是發現「微積分基本定理」的動機。
習題
- 若
是
在 [a, b] 區間內的積函數,請說明為什麼必然
?
- 若
是
在 [a, b] 區間內的積函數,而且
是正值的,請說明為什麼
必然漸增?
Created: Nov 15, 1996