定積分

若 在閉區間 [a, b] 內是一個連續函數 (不論正值或負值)，則它的積值必存在。 這叫做 柯西積分定理 (Cauchy integral theorem)。我們以後再來證明。 此積值稱為 在 [a, b] 內的 定積分 (definite integral)，記做

我們已經知道，若 在 [a, b] 內是正值的，則定積分值 (積值) 就是曲線下的面積。 如果 在 [a, b] 內是負值呢？ 回顧積分的原始意義 (之一)：

如果在 [a, b] 內 則 就是

(在 [a, b] 內由 和 x 軸圍成的區域之面積)

習題

1. 請問
   
   
   
   
2. 請問 (不需要知道 sin(x) 的反導函數就能回答)
   
   
   
   
3. 請問 (不需要知道 cos(x) 的反導函數就能回答)
   
   
   
   
4. 如果 a 是一個正數， 在 [-a, a] 內是一個連續函數而且是奇函數，請問
   
   
   
   有什麼必然的結果？為什麼？
5. 參照右側圖形，請判斷
   
   
   
   是正值還是負值？
   
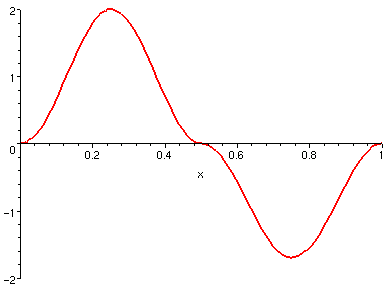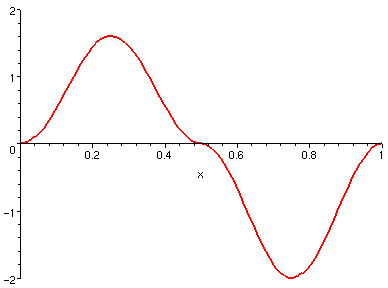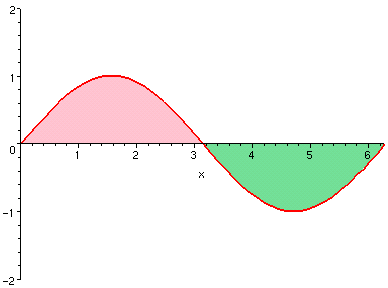
6. 參照右側圖形，請判斷
   
   
   
   是正值還是負值？