微分的線性性質

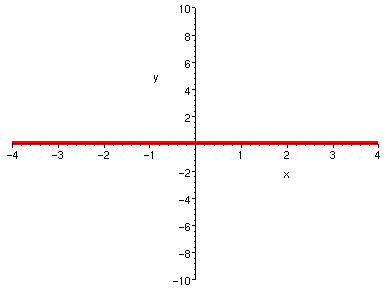
直接應用極限的線性性質，就可以推得微分的線性性質 (linearity of differentiation)。 這個性質的意思就是說，如果 和 在開區間 (a, b) 內有導函數，而 c 是任意一個實數， 則在區間 (a, b) 內：

因為上述性質的證明非常簡單而且直接， 我們就只開一個頭，由讀者去繼續完成。 對於常數的乘法性質，我們要知道，根據導數的定義：

根據微分的線性性質，再配合冪數為正整數 (或零) 的導函數公式， 我們立刻可以得知，多項式都在整個實數上可微，而且多項式的導函數少一階的多項式 (直到零階為止)：

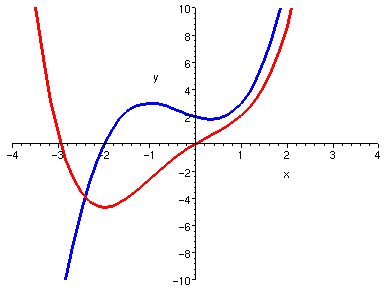
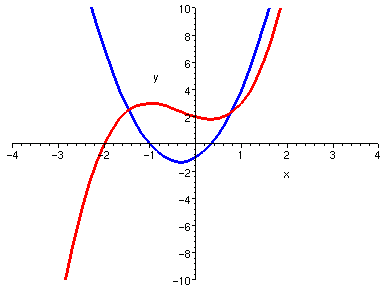
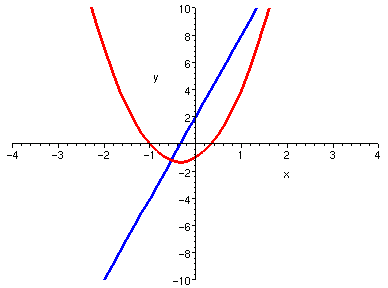
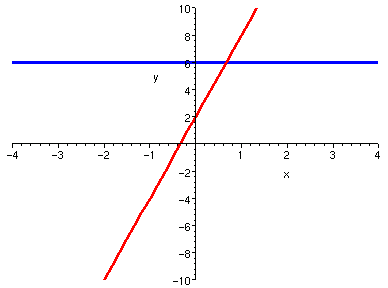
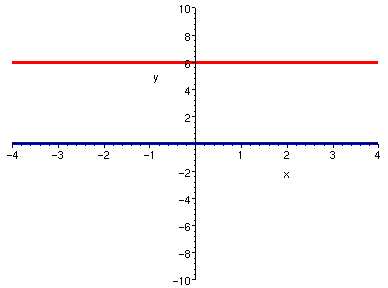
對照觀察多項式之曲線與其導函數曲線的關係，可以發現許多關於導數的意義。 而且有趣的是，如果持續將多項式的導函數再做導函數， 則階數越來越少，曲折也就越來越少，最後變成零函數。 這些性質以後都還會在其他講義看到，但是，針對多項式這種簡單的特例，我們先睹為快。 以下圖片中，藍色曲線是紅色的導函數。觀察

• 導數是正數時，原函數漸增。
• 導數是負數時，原函數漸減。
• 導數是零時，原函數在那一瞬間不增不減，可能發生曲折。
• 導函數漸增時，原函數凹向上。
• 導函數漸減時，原函數凹向下。

x^4/4 + x^3/3 - x^2/2 + 2*x	x^3 + x^2 - x + 2
3*x^2 + 2*x - 1	6*x + 2
6	0

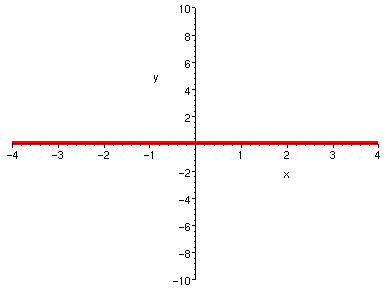
習題

1. 證明微分的常數乘法性質。
2. 證明微分的加法性質。
3. 如果 是 在 [a, b] 內的積函數，c 是隨便一個常數。證明
   
   
   
   
4. 請問
   
   
   
   
5. 請問
   
   
   
   
6. 請問
   
   
   
   
7. 請問
   
   
   
   
8. 請問 在 [1, 10] 內的積函數是什麼？ 小心，這個題目有陷阱，注意積函數在 x = 1 處必須是 0。