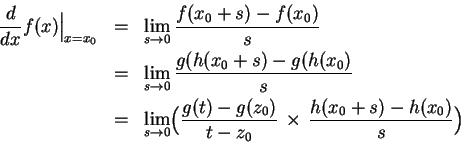
令
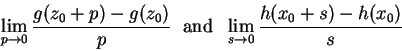
都存在,因此才能在以下引用極限的乘法律。 有了這些說明,就可以繼續完成我們的證明了:
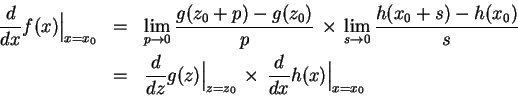
故得證。
如果
證明的步驟也很直接。
在以下證明當中,我們令
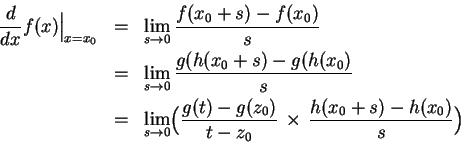
令 ![]() ,
也就是
,
也就是
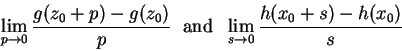
都存在,因此才能在以下引用極限的乘法律。
有了這些說明,就可以繼續完成我們的證明了:
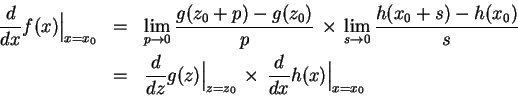
故得證。
微分連鎖律有一個容易一點的記法。回顧前面所說得簡寫方式:
連鎖律可能是所有微分運算規律當中最重要的一個了。
求
也可以看成
![]() 其中
其中
![]() 而
而
![]() 所以
所以
![]()
顯然地,兩個作法的結果相同。
求
也可以看成
![]() 其中
其中
![]() 而
而
![]() 所以
所以
![]()
顯然地,兩個作法的結果相同。
以下函數
現在,應用微分連鎖律,我們可以推導冪數為正有理數之冪函數的導函數公式。 令 n 和 m 是 (互質的) 正整數, r = m / n,則
令 r 是正有理數,則
連鎖律將是最主要的微分運算規律。 它看來頗複雜,但是大部分的步驟可以心算帶過, 而不必一步步地按照上述的範例進行。 就好像小學生做除法,本來需要按照九九乘法表一一測驗商數應該是多少, 但是熟練之後,就可以心算了。 熟能生巧,多練習是唯一的掌握這個技巧的辦法。
這裡我們只示範了兩個函數合成之後的連鎖律。 實際應用的時候,有可能需要三個、四個函數合成的連鎖律。 讀者應該可以舉二反三的。 太過複雜的導函數,我們將可以藉助於電腦軟體來做。 學生只要能心算或筆算較為簡單的導函數就足夠了。
令 h 是個很小的正數,考慮以 r+h 為外徑、以 r 為內徑的圓環面積,再除以 h。