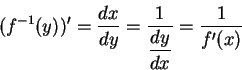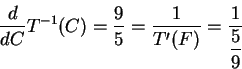反函數微分律
如果
因為
和
的曲線互相以 45 度角的直線為鏡射,所以它們的切線也是以此直線為鏡射。
因此,不難想像,這兩條互相鏡射的切線斜率互為倒數。參照以下示範圖片。
證明的步驟也很直接。假設
而且
在 x 0 有反函數,這表示
在 x 0 附近不是漸增就是漸減,
所以它在 x 0 的導數不是正數就是負數,
總而言之
這是一個關鍵。然後,在以下證明當中,我們令
也就是說
並且在倒數第二步採用變數變換
這樣,就應該可以讀懂以下的證明了:
反函數微分律有一個容易一點的記法。
如果簡寫
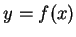 和
和
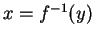 則反函數微分律就可以簡寫成
則反函數微分律就可以簡寫成
上面一串等式的中間兩項,
展現了萊布尼茲符號的漂亮用法:
它使得反函數微分律「看起來」好像是分數的倒數關係一樣。
我們必須在強調一下:「看起來」,其實當然不是那個意思。
不過,只要「看起來」好像,就很方便我們記憶了。
舉一個極簡單的例子。
攝氏溫標 C 與華氏溫標 F 之間的換算關係,
就是一個線性函數:
則 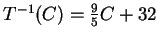 ,
因此
,
因此
現在,應用反函數微分律,我們可以推導根次冪函數的導函數公式。
令 n 是正整數,則開方根函數
的反函數是
所以
因此
所以,現在可以推廣冪函數的導函數公式如下:
令 n 是正整數,則不論 r = n 或 r = 1 / n,
都是
習題
- 求以下函數的導函數。
- 求以下函數的反導函數。
- 求以下函數的導函數。
- 請問
- 求以下函數的導函數。
- 請問
- 若
則將它微分七遍之後的導函數是什麼?
- 若
請問它的曲線在哪些區間內漸增 (也就是導數 >= 0)?[HH]
- 若
請寫出它的所有斜率為 5 的切線方程式。[HH]
- 若
請寫出它的所有通過原點的切線方程式。[HH]
- 單擺的週期 T 與擺長 s 之關係如下:
其中 g 是重力常數。請寫出
Created: Nov 20, 1996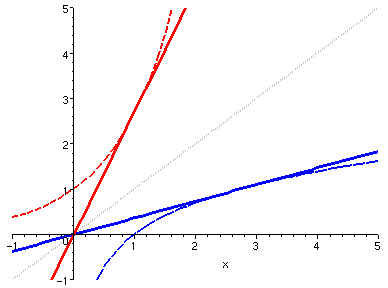



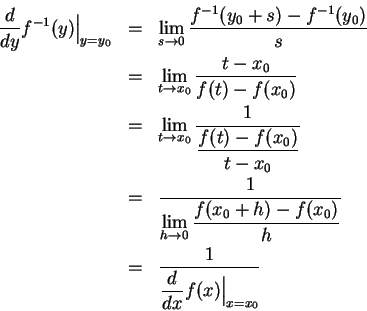
![]() 和
和
![]() 則反函數微分律就可以簡寫成
則反函數微分律就可以簡寫成