自然對數的算法

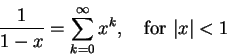
回顧無窮等比級數的和


可以改寫成以下「部分和加上誤差項」的形式：

其中 誤差項 (error term) 就是

換句話說，1/(1-x) 就「差不多」是無窮級數的 部分和 (partial sum)：

而這個「差不多」的誤差，就是 r n。

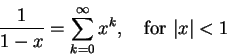
現在，將等式兩邊都在 [0, 1) 內做積函數，就是


運用連鎖律，讀者應該知道 所以上式就成了

其中誤差項是

現在，我們暫時不談此誤差項 只簡單地請讀者暫時相信

也就是說，當計算的項數 n 越來越多的時候，誤差就越來越小。 因此，自然對數就可以用以下公式估計出來，

而估計的誤差就是 。 這個公式不像以前我們看過的公式：它不是「封閉型式」的。 它並沒有告訴你確定的計算次數。它說，如果你要算得更精確， 就多算幾項；如果不需要太精確，就少算幾項。 而重點是，因為誤差終將趨近於 0，所以不論你需要多精確， 只要你算得夠多，就可以達到那個精度。 這裡所謂的「精確」就是指「小數點下有幾位可靠的位數」。

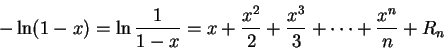
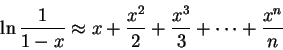
根據以上公式，對任何正數 t，如果 我們取 則 因此就可以代入公式：


而如果 那就令 那就還是符合 於是可以代入公式：

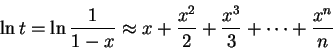
舉例來說，我們看以下的計算結果：
nt=2t=3t=4t=5t=6
100.6930648562 1.0958692095 1.3736579214 1.5788746667 1.7368363533
200.6931471371 1.0985858855 1.3858911585 1.6075458671 1.7865681007
300.6931471805 1.0986119711 1.3862784634 1.6092945006 1.7911632702
400.6931471806 1.0986122844 1.3862936717 1.6094259965 1.7916846298
500.6931471806 1.0986122886 1.3862943295 1.6094368684 1.7917495770
600.6931471806 1.0986122887 1.3862943596 1.6094378177 1.7917581166
700.6931471806 1.0986122887 1.3862943610 1.6094379036 1.7917592798
800.6931471806 1.0986122887 1.3862943611 1.6094379116 1.7917594422
900.6931471806 1.0986122887 1.3862943611 1.6094379124 1.7917594653
1000.6931471806 1.0986122887 1.3862943611 1.6094379124 1.7917594687
1100.6931471806 1.0986122887 1.3862943611 1.6094379124 1.7917594691
1200.6931471806 1.0986122887 1.3862943611 1.6094379124 1.7917594692

讀者很容易觀察，對任何 t 此公式都越算越多位數不再改變， 這些位數就是可靠的數值，或者說是「已經收斂」的部分。 t 越大，收斂得稍微慢些，但是總歸還是會收斂。 這就是自然對數的算法了。

這一節的習題，是加深練習對數函數的微分與積分， 並不直接與這一講的內容有關。

習題

  1. 請問


  2. 利用函數的奇偶性質，以及積分的意義，回答以下問題：


  3. 請問


  4. 利用函數的奇偶性質，以及積分的意義，回答以下問題：


  5. 請問


  6. 請問


  7. 請推導


Created: Aug 14, 2001
Last Revised: Aug 14, 2001
© Copyright 2001 Wei-Chang Shann 單維彰