等比級數
令 x 是個實數,回顧以下等比級數的定義和符號:
其中 x 稱為公比。
讓我們將此級數的和簡記為
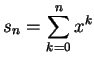 那麼,可以用以下方法求和。先在 (1) 式兩邊都乘 x,得到
那麼,可以用以下方法求和。先在 (1) 式兩邊都乘 x,得到
然後讓 (1) 式減 (2) 式,所以
亦即
上式對所有正整數 n 與所有不是 1 的實數 x 均成立。
如果將 (1) 式中的項數推到無窮多,
就成了「無窮等比級數」,它的意義是
因為
上面那個極限,只有當 -1 < x <= 1 時收斂。
(當 x = -1 時,
所以數列是 1, -1, 1, -1 這樣的跳動,所以直覺地知道它的極限不存在。)
但是當 x = 1 時,分母無意義。
所以
這就是無窮等比級數的基本公式。做一點推廣,就是
其中 n 是任何正整數。
習題
- 證明
- 請問
- 請將以下方程式寫成一個無窮級數的和。
- 請問
- 請問
- 請問
- 請問
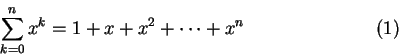
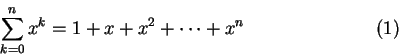
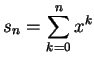 那麼,可以用以下方法求和。先在 (1) 式兩邊都乘 x,得到
那麼,可以用以下方法求和。先在 (1) 式兩邊都乘 x,得到
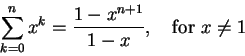
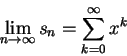
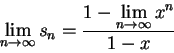
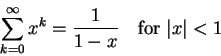
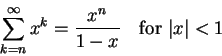
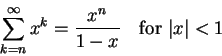
Created: Aug 14, 2001