關於泰勒級數的 Maple 指令

指令 series(f(x), x=c, n) 輸出函數 在 附近的 階泰勒多項式 與其誤差項的代表。如果只寫了 x 就表示 x=0。例如

> series(sin(x), x, 6);

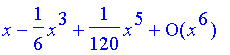
> series(log(x), x=1, 7);

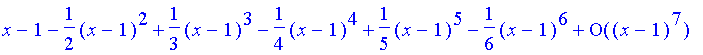
> series(1/(1-x), x, 8);

如果只想得到泰勒多項式，必須從泰勒展開裡面轉移出來。需要的指令是 convert(expr, polynom) 其中 expr 是一個泰勒展開，如下。

> P := series(sin(x), x, 6);

> p := convert(P, polynom);

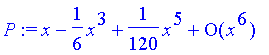
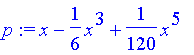
或者可以把兩句話合在一起說，如下。

> q := convert(series(ln(x), x=1, 7), polynom);

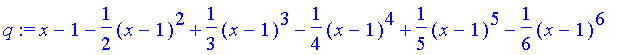
但是，這樣並不能使得 q 成為一個函數。如果想要它成為一個函數，可以說一個奇怪的指令 unapply 這個指令的基本型態是 unapply(expr, x); 意思是說，把 expr 裡面的符號 x 變成自變量，其中 x 可以改成任何適當的符號。例如

> q := unapply(q, x);

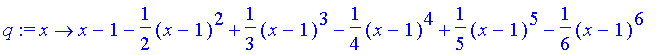
現在 q(x) 是一個函數了，因此可以試試看平移的效果：

> q(x+1);

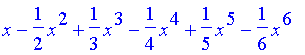
必須先將泰勒展開轉換成多項式，才能畫圖。 講義中的圖片，是以類似以下指令製作的。

> plot([q(x), ln(x)], x=0..3, y=-2..2, color=[red, pink]);

如果函數有垂直漸近線，那就是不連續，可以在製圖指令中用一個參數告訴 Maple。這樣它畫出來的圖 比較好看。例如

> plot(1/(1-x), x=-1..3, y=-5..5, discont=true);

現在，我們運用 Maple 的製圖功能，來觀察泰勒級數的收斂區間。 以下是以 5 階泰勒多項式為例，讀者可以自行改變多項式的階數，然後觀察。

> s := unapply( convert( series(1/(1-x), x, 6), polynom), x):

> plot([s(x), 1/(1-x)], x=-2..3, y=-5..5, discont=true, color=[red,pink]);

>

習題

1. 請寫出讓 Maple 輸出 在 x = 0 「附近」的七階泰勒多項式的指令。
2. 請猜測 在 x = 0 「附近」的泰勒級數之收斂半徑。
3. 請寫出讓 Maple 輸出 在 x = 0 「附近」的七階泰勒多項式的指令。
4. 請猜測 在 x = 0 「附近」的泰勒級數之收斂半徑。
5. 請寫出讓 Maple 輸出 在 x = 0 「附近」的七階泰勒多項式的指令。
6. 請猜測 在 x = 0 「附近」的泰勒級數之收斂半徑。