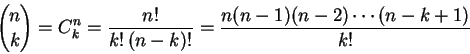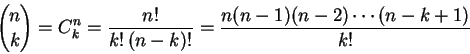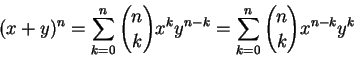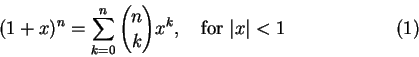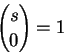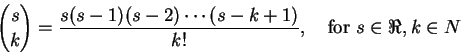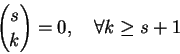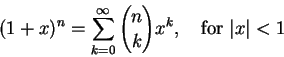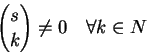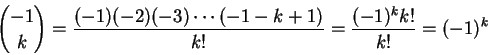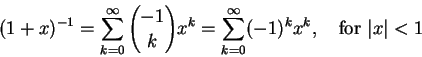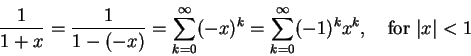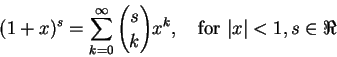二項級數
回顧二項係數 (binomial coefficient) 的定義:
根據此定義,很明顯地
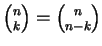 所謂二項係數這個名詞,來自於它們是二項式展開的係數,如下:
所謂二項係數這個名詞,來自於它們是二項式展開的係數,如下:
因為
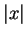 和
和
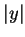 兩數之間,總有 一個比較小,就說是
兩數之間,總有 一個比較小,就說是
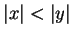 吧 (如果兩個數一樣,那麼就成了 0n 或者
吧 (如果兩個數一樣,那麼就成了 0n 或者
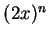 根本沒有「二項式」可談了)。那麼,我們可以令
根本沒有「二項式」可談了)。那麼,我們可以令
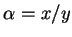 所以二項式可以拆成
所以二項式可以拆成
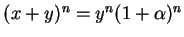 因此,我們認識到,其實只要考慮以下二項式就夠了:
因此,我們認識到,其實只要考慮以下二項式就夠了:
從二項係數的定義來看,只要 k 是個非負整數,
那麼即使 n 不是個正整數也沒關係。
若 s 是個實數,則可以定義
和
如果 s 是個非負整數,則
所以 (1) 式就算寫成一個無窮級數也可以:
但是,如果 s 不是非負整數,那些二項係數就沒完沒了,也就是說
讓我們試試看 s = -1 吧,那些二項係數就是
所以,如果套用二項式展開公式,就得到
另一方面,回顧無窮等比級數公式,代入 -x 就得到
嘩,多麼美妙的巧合啊!
牛頓在三十歲以前,就發現了這個巧合,而且他很快地確信,
一般而言,這個無窮多項的二項式展開都是對的:
這就是 二項級數 (binomial series)。
三十多年以後,牛頓的學生泰勒發現這是他的「泰勒級數」的一種特例。
讓我們看看
Created: Aug 17, 2001