數學中最美的等式
請回想虛數單位元素
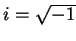 的整數次方有「四段輪迴」的性質:
的整數次方有「四段輪迴」的性質:
也就是說,
因此,將
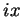 代入指數函數在 0 附近的泰勒級數,得到
代入指數函數在 0 附近的泰勒級數,得到
現在,我們把偶數項 (也就是實數項) 集合在一起,把奇數項 (也就是虛數項)
集合在一起,就得到如下的級數:
您是否像歐拉 (Euler) 當年一樣,發現了以下這個有趣的等式?
其實,現代數學還要擔心一個嚴格的問題:
一個無窮級數能不能隨便改變它各項相加的順序,而保持同樣的和?
當年的歐拉並不警覺有這個問題,他就這麼做了。
後代的數學家,在嚴格證明之後,同意歐拉這樣做是對的。
關於上述等式,我們暫且稱其「歐拉等式」,
我們可以獲得一些立即而實用的計算法。
首先,就是被稱為棣美弗定律的等式:
棣美弗並沒有使用歐拉等式,就用高明的辦法發現了以上等式,
但是,利用歐拉等式,它就變得簡單極了。
因為正弦是奇函數而餘弦是偶函數,所以
因此
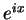 的共軛複數就是
的共軛複數就是
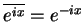 又因為
又因為
所以我們看到,
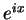 其實就是複數平面之單位圓上的一個點,而它與實軸的夾角是 x。
其實就是複數平面之單位圓上的一個點,而它與實軸的夾角是 x。
現在,將 x 代入特殊角
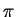 ,得知
,得知
現在,選美皇后要揭曉了:
數學中最美的等式就是•••
為什麼她最美?數學家可以舉出好幾個理由:
- 因為她短。數學家喜歡越短越好。
- 因為她表現了數學中最重要的三個單位元素:0 和 1 和 i。
- 因為她表現了數學中最重要的兩個常數:
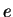 和
和
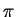 。
。
- 因為她表現了數學中最重要的運算:加法,乘法,次方。
- 因為她表現了數學中最重要的觀念:「什麼是等於?」。
很美吧?
習題
- 請問
- 請問
- 請推導
- 請推導
- 請推導
其中
Created: Aug 17, 2001![]() 的整數次方有「四段輪迴」的性質:
的整數次方有「四段輪迴」的性質:
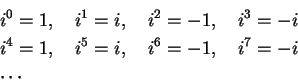
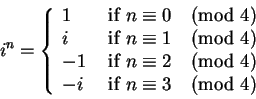
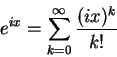
![]() ,得知
,得知