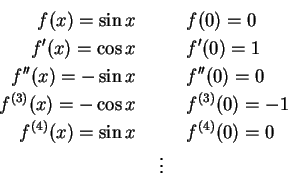
���ڭ̱q������ƶ}�l�C�����A�ڭ��[������ɨ�Ʀ��u�|�q���j�v���ʽ�G
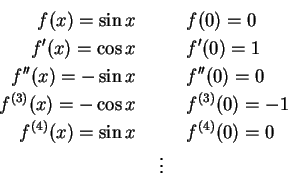
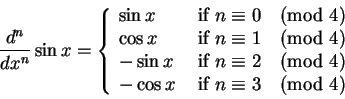
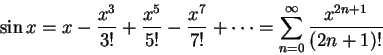
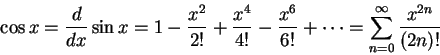
�H�U�A�ڭ̦b
![]() �e�X�����P�l���H 0 ���Ѧ��I�����Ǧh�����C
�H�⪺���u�O�����ξl�����u�C
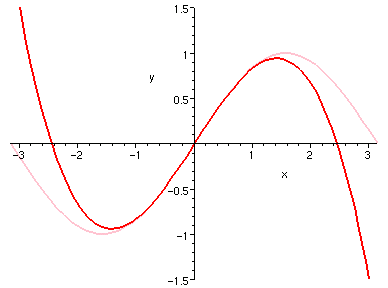
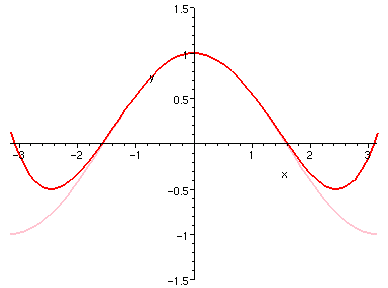
�e�X�����P�l���H 0 ���Ѧ��I�����Ǧh�����C
�H�⪺���u�O�����ξl�����u�C
| sin(x) 3 �� | cos(x) 4 �� |
|---|---|
| 
|
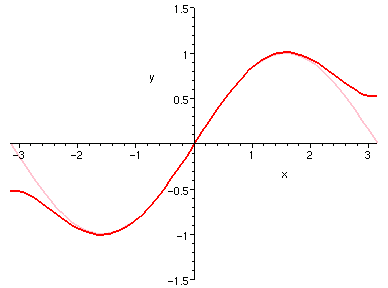
| sin(x) 5 �� | cos(x) 6 �� |
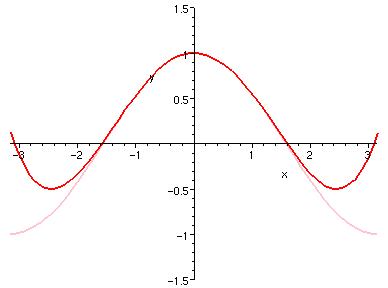
| 
|
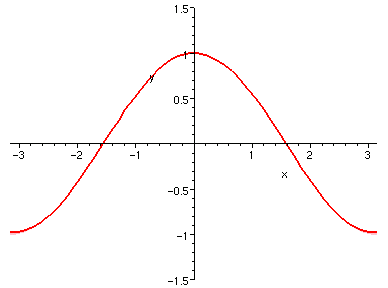
| sin(x) 7 �� | cos(x) 8 �� |
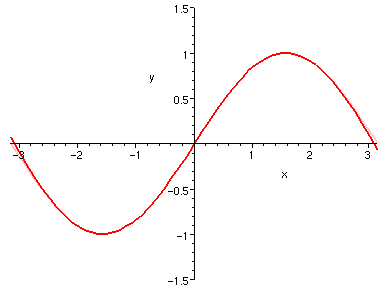
| 
|
�{�b�A�ڭ̧Q�ΤG���żƥH�ΤϾɨ�ơA���ɨ�ӤϤT����ƥH 0 ���Ѧ��I�����ǯżơC
�����A�Ʋ�
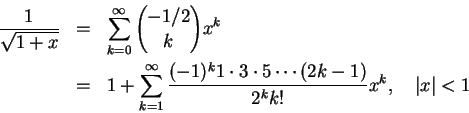
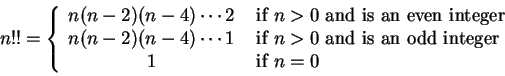
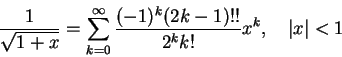
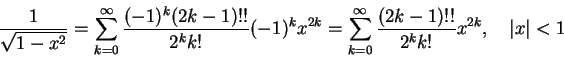
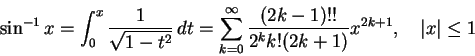
�]��
![]() �ҥH�ϥ��������ǯżơA���K���ڭ̧��F�@�ӭp���P�v��p���I�U���N�h�쪺��k�C
�]�N�O
�ҥH�ϥ��������ǯżơA���K���ڭ̧��F�@�ӭp���P�v��p���I�U���N�h�쪺��k�C
�]�N�O
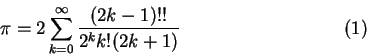
�䦸�A�b�ƲߵL�a����ż�
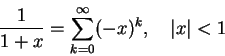
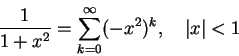
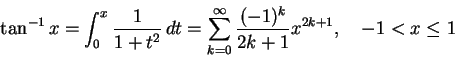
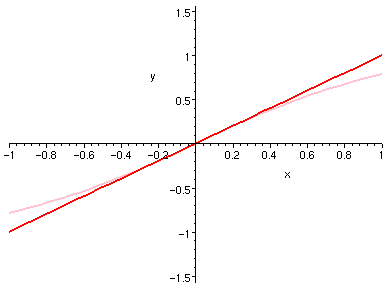
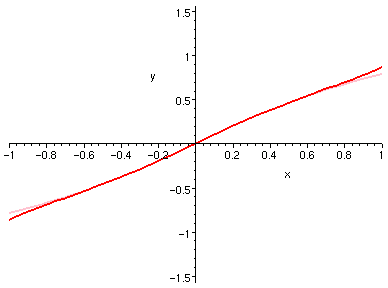
�H�U�A�ڭ̦b [-1, 1] ���e�X�ϥ����P�ϥ����H 0 ���Ѧ��I�����Ǧh�����C
�H�⪺���u�O��Ӫ���ơC
| arcsin(x) 1 �� | arctan(x) 1 �� |
|---|---|
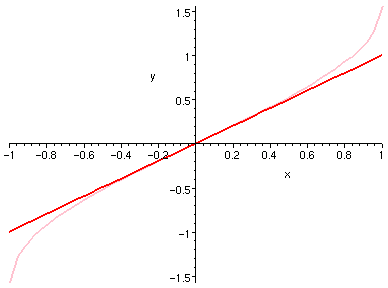
| 
|
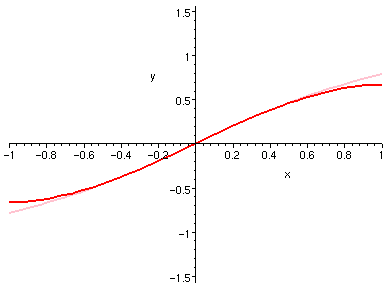
| arcsin(x) 3 6� | arctan(x) 3 �� |
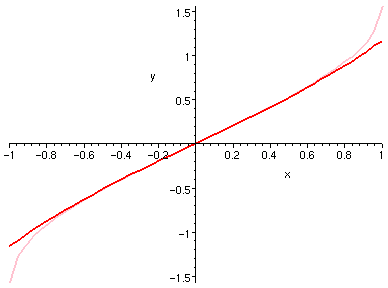
| 
|
| arcsin(x) 5 �� | arctan(x) 5 �� |
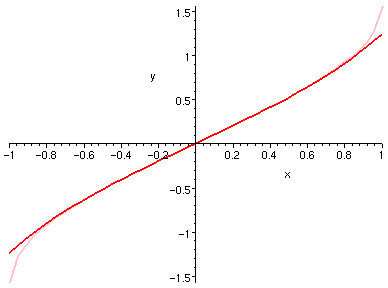
| 
|
�H�W�ϥ����P�ϥ��������ǯżơA���i�H�ѥ��̪��ɨ�ƨD�o�A �u�O�A�q�G���żƨӿn���A�����K�C �ӥB�A�o�O������y�Ҹg�����߸����{�C �b�~�������y�o�{�o�Ǥ������ɭԡA�����٨S�X�͡A �ӥB���y�]�S���o�{�����ǯżƳo�˪��@������Y�C �L�O�q�G���żƱo��F�ϤT����ƪ��żƭp�⤽���A �A�ϹL�ӨD�ѥ�����ƪ��żƭp�⤽���C �ҥH�A���y���M���D�����P�l�����żơA �o���O�Χڭ̤��ѩһ��o���Ǯi�}�o�쪺�C
�b (1) �M (2) �o�حp�⤽���X�{�H�e�A
�@�ɤW�p���P�v�������O���H�O����n�_�®ɥN�����R���A
�L�p�⪺�u�K�v�v�O 355/113�A�X�p�Ƥj�� 3.14159292�A
�ǽT��p���I�U�Ĥ���C
�o�ӼƾګO���@�ɰO���j�� 1000 �~�C
�@���� (1) �M (2) �o�ؤ����X�{�F�A����H�u�n�V�O�h��A
�N��}�o�Ӭ����C
���O�A�o��Ӥ��������ıo����֡A�� (2) ������ (1) �֡A�ӥB�����n�ݡA
�ҥH���O�̵ۦW����P�v�p�⤽���C
�ƹ�W�A���� (2) �b���y���e�N�Q�o�{�F�A
�u�O���ɭԭn��n�@�f�\�Ҥ~��o��A
�Ӳ{�b�z�L�ϥ�����ơA�ܤ�K�N�i�H�A�ѤF�C
�H�U�A�ڭ̦C�X (1) �M (2) �p���P�v���ƭȵ��G�C
| n | 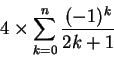
| 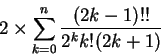
|
|---|---|---|
| 10 | 3.2323158094 | 2.8001699635 |
| 100 | 3.1514934011 | 3.0292687383 |
| 1000 | 3.1425916543 | 3.1059265157 |
| 104 | 3.1416926436 | 3.1303093791 |
| 105 | 3.1416026535 | 3.1380244217 |
| 106 | 3.1415936536 | 3.1404642749 |
| 107 | 3.1415927536 | 3.1412358288 |