若
則取了倒數之後,就是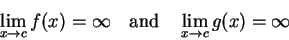 所以很自然地
所以很自然地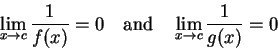 就成了
就成了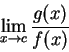
的不定型式。 因此,我們知道,無論是
還是 的不定型式,都可以直接使用羅必達法則。 這裡我們舉兩個例子:
還有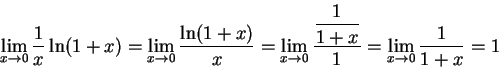
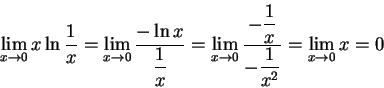
除了
不論哪一種不定型式,總是可以設法轉換成
若
因此,我們知道,無論是
這裡我們舉兩個例子:
則取了倒數之後,就是
![]() 所以很自然地
所以很自然地
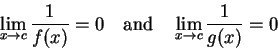 就成了
就成了
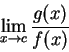 還有
還有
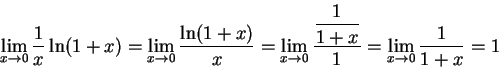
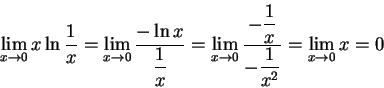
以下這個例子,其實有更簡單的解法 (因式分解),
但是我們故意使用羅必達法則以作為練習。
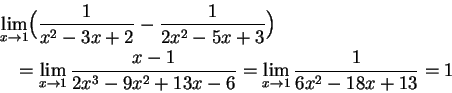
務必先確定極限屬不定型式,才要使用羅必達法則。不要盲目地用。
我們現在還沒有必要談