積分的線性、方向性、銜接性和保序性
首先,我們再度複習柯西 (Cauchy) 型式的積分定義。
先是給定一個閉區間
![$[a,b]$](img11.gif) 和一個正整數 n,我們將
和一個正整數 n,我們將
![$[a,b]$](img11.gif) 均勻切割 (uniform partition) 成 n 等分。
每一等分的寬度就是
均勻切割 (uniform partition) 成 n 等分。
每一等分的寬度就是
符號
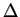 唸做 delta,它是希臘字母
唸做 delta,它是希臘字母
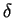 的大寫符號。而分割這 n 等分的 n + 1 個點,
稱為 節點 (nodal point),它們是
的大寫符號。而分割這 n 等分的 n + 1 個點,
稱為 節點 (nodal point),它們是
換句話說,它們也就是
在這 n 等分上,我們以
![$[x_{k-1}, x_k]$](img6.gif) 為寬、以
為寬、以
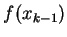 為高,做成 n 個矩形。令這 n 個矩形的面積和是
為高,做成 n 個矩形。令這 n 個矩形的面積和是
而所謂的 柯西積分定理 (Cauchy integral theorem) 就是說
如果
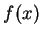 是
是
![$[a,b]$](img11.gif) 閉區間內的連續函數,則
閉區間內的連續函數,則
極限收斂到一個實數 I,而它就是
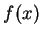 在
在
![$[a,b]$](img11.gif) 內的積分值,記做
內的積分值,記做
而我們稱
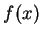 在
在
![$[a,b]$](img11.gif) 內「可積」(integrable)。
內「可積」(integrable)。
另一方面,微積分基本定理說,如果
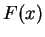 是
是
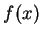 的反導函數,亦即
的反導函數,亦即
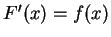 ,
則
,
則
以下介紹定積分的四個基本性質。
- 線性 (Linearity)
若 c 是一個實數,而
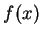 和
和
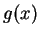 on ab
都在
on ab
都在
![$[a,b]$](img11.gif) 內可積。則直接根據上述 Ln 的定義以及極限的線性性質,
就能瞭解:
內可積。則直接根據上述 Ln 的定義以及極限的線性性質,
就能瞭解:
和
這兩個性質 (以上的加號,若
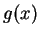 on ab
換成
on ab
換成
習題
- 如果
而且
請問
- 定義 標準正規分佈函數 如下:
如果給定以下估計值表格:[HH]
請問
- 定義 標準正規分佈函數 如下:
如果給定以下估計值表格:[HH]
請問
- 定義 標準正規分佈函數 如下:
如果給定以下估計值表格:[HH]
請問
[提示:考慮 N(x) 是奇偶性質?]
- 說明為什麼
- 說明為什麼
Created: Aug 20, 2001![]() 和一個正整數 n,我們將
和一個正整數 n,我們將
![]() 均勻切割 (uniform partition) 成 n 等分。
每一等分的寬度就是
均勻切割 (uniform partition) 成 n 等分。
每一等分的寬度就是
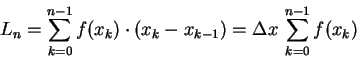
是
閉區間內的連續函數,則
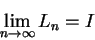
在
內的積分值,記做
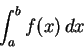
在
內「可積」(integrable)。
![]() 是
是
![]() 的反導函數,亦即
的反導函數,亦即
![]() ,
則
,
則
![]() 和
和
![]() on ab
都在
on ab
都在
![]() 內可積。則直接根據上述 Ln 的定義以及極限的線性性質,
就能瞭解:
內可積。則直接根據上述 Ln 的定義以及極限的線性性質,
就能瞭解: