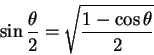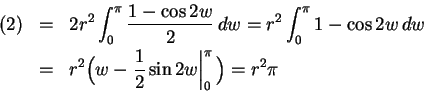定積分之變數變換

如果要採用變數變換的技巧做定積分，我們有兩種作法：

將原來變數的積分上下限 a 和 b 換成 w(a) 和 w(b)，在求得 g(w) 的反導函數後，直接以 w(a) 和 w(b) 代入求定積分值。例如

令所以、因此
先對 w 做不定積分，將結果寫回到原來的變數 x 之後，再代入原來的積分上下限。例如 (1) 式也可以這樣做：

因此

現在，我們終於可以用微積分方法求圓的面積了。考慮以原點為圓心，以 r > 0 為半徑的圓，它的隱函數方程式是

$\begin{displaymath} x^2 + y^2 = r^2 \end{displaymath}$

其顯性方程式是

$\begin{displaymath} y = \pm\sqrt{r^2-x^2},\quad\mbox{for}\quad -r\leq x\leq r \end{displaymath}$

但因為圓是上下對稱的，所以，只要計算上半圓的面積，再乘以二即可。因此，以下就是圓的面積計算積分式：

$\begin{displaymath} 2\int_{-r}^r \sqrt{r^2-x^2}\,dx \eqno(2) \end{displaymath}$

稍微整理一下，得到

$\begin{displaymath} (2) = 2r\int_{-r}^r \sqrt{1-\bigl(\frac{x}{r}\bigr)^2}\,dx \end{displaymath}$

做變數變換，令

$\begin{displaymath} \frac{x}{r} = \cos w,\quad\hbox{for}\quad w\in[0,\pi] \end{displaymath}$

則

$\begin{displaymath} x=-r\;\Rightarrow\; w = \pi\quad\mbox{and}\quad x=r\;\Rightarrow\; w=0 \end{displaymath}$

而且，運用隱函數微分，得到

$\begin{displaymath} \frac1r = -\sin w\,\frac{dw}{dx} \end{displaymath}$

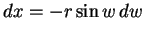所以 $dx = -r\sin w\,dw$ 因此

$\begin{displaymath} (2) = 2r\int_{\pi}^0 \sqrt{1-\cos^2 w}\bigl(-r\sin w\,dw\bigr) = 2r^2\int_0^{\pi} \sqrt{\sin^2 w}\,\sin w\,dw \end{displaymath}$

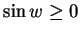因為對所有的 $w\in[0,\pi]$ 都是 $\sin w \geq 0$ ，所以我們可以開根號，繼續

$\begin{displaymath} (2) = 2r^2 \int_0^{\pi} \sin^2 w\,dw \end{displaymath}$

運用半角公式：

$\begin{displaymath} \sin\frac{\theta}2 = \sqrt{\frac{1-\cos\theta}2} \end{displaymath}$

我們終於得到

$\begin{eqnarray*} (2) &=& 2r^2\int_0^{\pi} \frac{1-\cos 2w}2\,dw = r^2\int_0^{\p... ...l(w - \frac12\sin 2w\biggl.\biggr\vert _0^{\pi}\,\Bigr) = r^2\pi \end{eqnarray*}$

您看，我們使用了好多技術，可見圓的面積不是個簡單問題啊。

習題

請問
請問
請問
請問
請問
請問
請問
請問
請用微積分方法計算以下橢圓的面積。