這一篇的主題是介紹閉區間中連續函數所特有的性質， 我們不證明這些性質（至少在這一篇中不證明），但是希望能給讀者一個初步的概念， 瞭解為什麼會有這些性質？而如果函數在閉區間中不連續， 或者連續但不是在閉區間中，為什麼就沒有這些性質？
如果存在一個正實數 M 使得 f(x) 在某個 x 的範圍內符合
閉區間中的連續函數都有界：
若 f(x) 是 [a,b] 區間中的連續函數，則存在一個正實數 M 使得
中間值定理是說，若 f(x) 是閉區間 [a,b] 內的連續函數， 則 f(x) 會映射到 f(a) 與 f(b) 之間的每一點。 直覺地看，如果 x 代表時間而 f(x) 代表位置， 則物體若從時間 a 所在的 f(a) 點移動到時間 b 所在的 f(b) 點， 它當然會經過 f(a) 與 f(b) 之間的每一點。 它有可能在 f(a) 與 f(b) 之間來回往返了好幾回， 還甚至有可能跑到比 f(b) 更遠的地方再折回 f(b)，但是這些我們都不知道， 也不去管，我們可以肯定的是，它經過了 f(a) 與 f(b) 之間的每一點至少一次！ 數學的敘述是：
若 f(x) 是 [a,b] 區間中的連續函數，則對任何一點 都存在一個 使得
中間值定理有一個重要的推論，就是說
若 f(x) 是 [a,b] 區間中的連續函數，而且如果 則 f(x) 在 [a,b] 內有一個根；也就是說，存在一個數 使得
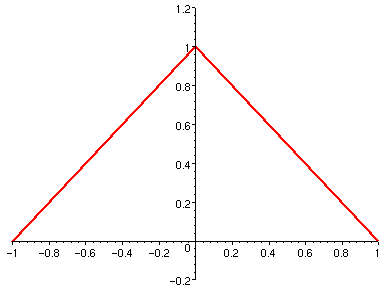
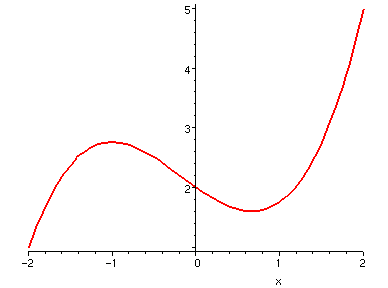
若 f(x) 是 [a,b] 區間中的連續函數，則存在一個數 使得 我們稱 f(x) 在 處有最大值，而 是 f(x) 在 [a,b] 內的最大值。
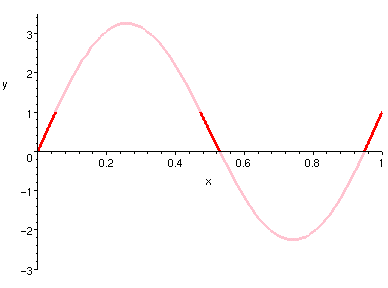
也有人會不假思索地假設，如果 f(x) 有最大值，那個最大值是唯一的。 再仔細一點想，就知道這是謬誤的概念。 譬如 sin(x) 在 之內，就有 4 處發生最大值，請讀者自己找到那四處。
相對於最大值定理，還有個最小值定理，但是我們將它留作習題。
這是我們已經在別的講義中說過的事，在此提醒一遍。 簡單地說，就是閉區間中的連續函數必可積。 如果這個函數找得到反導函數，那就好辦； 如果找不到，就得要回歸「曲線下面積是小矩形的面積和」這個基本看法。 而這個看法牽涉到一個無窮數列，而無窮數列就有極限不存在、發散或收斂的情形。 柯西積分定理就是說，別擔心，對於閉區間中的連續函數， 這個數列必定收斂。 在別的講義中，我們大概說的是一個比較簡單的形式。 現在說一個涵蓋比較廣泛的版本。
如果 f(x) 是 [a,b] 區間中的一個連續函數。 任選一個正整數 n，把 [a,b] 區間等分成 n 段，則每一段的長度是
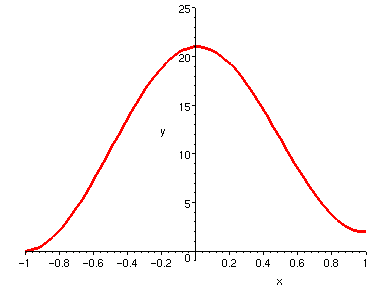
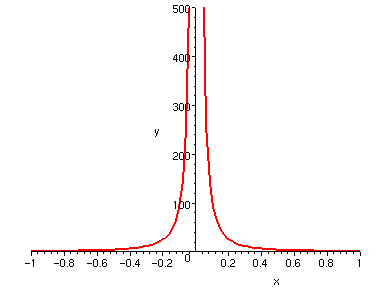
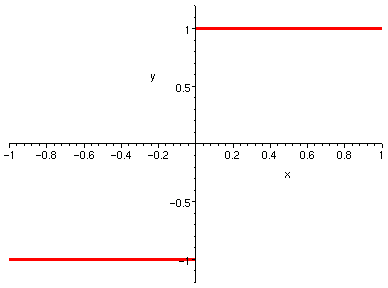
閉區間中的不連續函數，有以下兩種典型： 兩個都是 [-1,1] 閉區間中的不連續函數。 左邊的圖是在 x=0 處無定義，而且其趨近於 0 的極限發散。 右邊的圖是在 x=0 的左、右極限都存在，可是不相等。
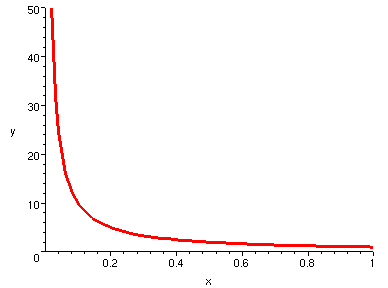
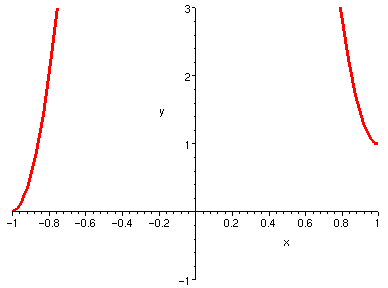
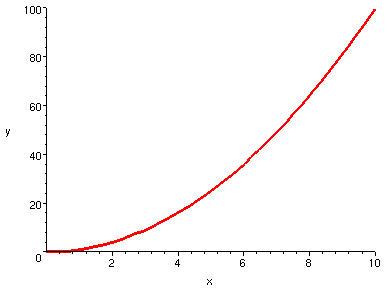
非閉區間中的連續函數，有以下兩種典型。 左邊的圖是在 (0,1] 中的連續函數，它在 x=0 處不需要定義， 因為我們根本不考慮 x=0 這一點的函數值 (它不在函數的定義域內)。 右邊的圖是在 中的連續函數。 1/x x^2 上面兩張圖，都顯然不符合「有界」和「最大值」定理。 至於中間值定理，因為上面兩個函數所定義的區間沒有「左端點」或是沒有「右端點」， 所以就不必談「介於兩端點的函數值」了。 但是，以上兩個函數是否分別在 (0,1] 中和在 可積呢？ 在這類的非閉區間中，它的積分又是什麼意思？ 我們不在這裡回答這些問題，暫時存疑。
為什麼會這樣呢？
那是因為我們假設 f(x) 在閉區間 [a,b] 上是連續的，所以
以上我們用了兩個希臘字母，