可補救的不連續函數
如果函數 f(x) 在 x=c 附近有定義,但是在 x=c 處不連續,
那麼很可能 f(x) 在 x=c 處無定義。就好像
這四個函數都在 x=0 處無定義。所以它們都在 x=0 處不連續。
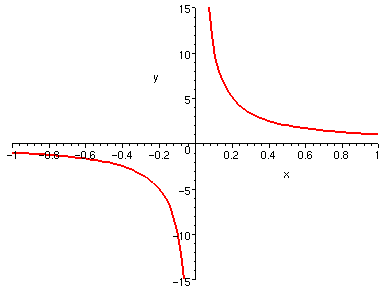
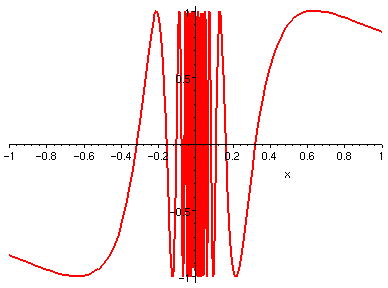
但是,看看它們的圖形,前兩個是很罪大惡極地不連續,
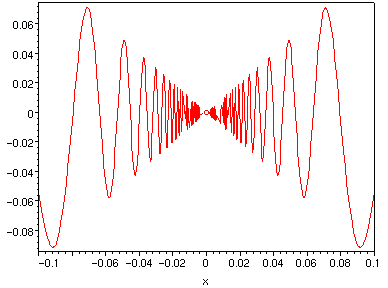
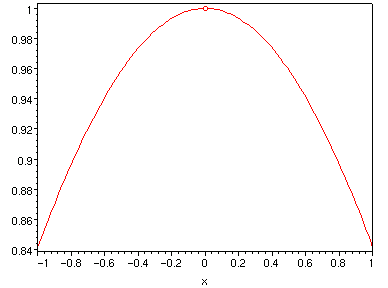
後兩個則似乎只差一個點就要連續了,說它不連續好像有點兒可惜。
| 1/x, x=-1..1 | sin(1/x), x=-1..1
|
|---|
| 
|
| x*sin(1/x), x=-1..1 | sin(x)/x, x=-1..1
|
|---|
| 
|
我們可以用數學語言,明白表達上述的看法。
- 如果 f(x) 在 x=c 處的極限發散或者不存在,則 f(x) 在 x=c 處的不連續,
屬於 不可補救的不連續 (或者說「無可救藥」的不連續如何?)
- 如果 f(x) 在 x=c 處沒有定義,但是在 x=c 處的極限卻存在,
則 f(x) 在 x=c 處的不連續屬於 可補救的不連續。
補救的方法,就是為它量身定做一個函數:定義 f(c) 的值就是函數在 x=c 處的極限。
例如我們已經知道
極限不存在,所以它們是不可補救的不連續。
但是 (根據夾擊定理或羅必達法則)
所以,我們只要規定
它就是個連續函數了。同理,因為 (夾擊定理與三角關係,或者用羅必達法則)
所以,我們只要規定
它就是個連續函數了。
習題
- 若定義
請問 f(x) 在 x=0 處是否連續?簡述理由。
- 若定義
請問 f(x) 在 x=0 處是否連續?簡述理由。
- 如果
在整個實數上都是連續函數,請問 A 應該是多少?簡述理由。
- 如果
在整個實數上都是連續函數,請問 A 應該是多少?簡述理由。
- 如果
在
Created: Aug 24, 2001






