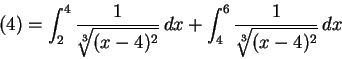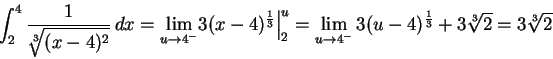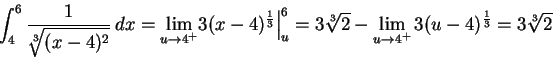無限大函數的廣義積分

無限大函數的廣義積分可以簡化成以下兩種問題來討論：

考慮 f(x) 在 [a,b) 區間中連續，而且在 b 點不能做連續拓展。也就是說，
考慮 f(x) 在 (a,b] 區間中連續，而且在 a 點不能做連續拓展。也就是說，

因為兩者的處理方式相同，我們只說第二者。

任給一個介於 a b 之間的數 u，則 f(x) 是 [u, b] 內的連續函數，所以可積，其定積分將是隨 u 而變的函數：

如果

收斂，則我們稱 f(x) 在 (a,b] 中可積，而其積分值就是上述極限。如果不收斂（極限不存在或發散），則稱 f(x) 在 (a,b] 中不可積。

例如考慮

$\begin{displaymath} \int_0^1 \frac1{\sqrt{x}}\,dx \eqno(1) \end{displaymath}$

很顯然，被積分函數是在 (0,1] 中的連續函數，而它是一個「無限大函數」類型的廣義積分。因此

$\begin{displaymath} (1) = \lim_{u\to0^+}\Bigl.2\sqrt{x}\Bigr\vert _u^1 =\lim_{u\to0^+} (2-2\sqrt{u}) = 2 \end{displaymath}$

所以問題 (1) 是可積的，積分值是 2。

再考慮一個非常類似的問題：

$\begin{displaymath} \int_0^1 \frac1{x}\,dx \eqno(2) \end{displaymath}$

它也是一個 (0,1] 中的「無限大函數」類型之廣義積分。但是

$\begin{displaymath} (2) = \lim_{u\to0^+}\Bigl.2\ln x\Bigr\vert _u^1 =- \lim_{u\to0^+} \ln u = \infty \end{displaymath}$

所以問題 (2) 是不可積的。

如果一個積分問題必須分割成兩個 (以上) 的廣義積分，那麼，這些廣義積分當中，只要有一個不可積，我們就說原來那個積分問題不可積。 例如 f(x) 在 [a,b] 中除了 x=c 處沒定義而且有垂直漸近線之外，在其他點上都連續。則

$\begin{displaymath} \int_a^bf(x)\,dx = \int_a^c f(x)\,dx + \int_c^b f(x)\,dx \end{displaymath}$

如果

$\begin{displaymath} \int_a^c f(x)\,dx \quad\hbox{or}\quad \int_c^b f(x)\,dx \end{displaymath}$

其中之一是不可積的，則我們就說 f(x) 在 [a,b] 中不可積。

例如考慮

$\begin{displaymath} \int_{-1}^1 \frac1x\,dx \eqno(3) \end{displaymath}$

顯然這個積分應該拆成兩段廣義積分來做：讀者要非常注意，不要誤以為

$\begin{displaymath} (3) = \ln\vert x\vert\Bigl.\Bigr\vert _{-1}^1 = 0\quad\hbox{\bf WRONG} \end{displaymath}$

這是錯誤的！正確的做法是

$\begin{displaymath} (3) = \int_{-1}^0\frac1x\,dx + \int_0^1\frac1x\,dx \end{displaymath}$

但是，上式右邊兩個廣義積分之一，就是問題 (2)，我們已經知道它不可積。因此問題 (3) 是不可積的。

最後，考慮

$\begin{displaymath} \int_2^6 \frac1{\root 3 \of {(x-4)^2}}\,dx \eqno(4) \end{displaymath}$

很明顯這個積分問題應該拆成 [2,4) 和 (4,6] 兩個「無限大函數」的廣義積分。

$\begin{displaymath} (4) = \int_2^4 \frac1{\root 3 \of {(x-4)^2}}\,dx + \int_4^6 \frac1{\root 3 \of {(x-4)^2}}\,dx \end{displaymath}$

現在，我們必須分別處理上式右邊的兩個廣義積分。因為

$\begin{displaymath} \int_2^4 \frac1{\root 3 \of {(x-4)^2}}\,dx =\lim_{u\to4^-}\B... ...lim_{u\to4^-} 3(u-4)^{\frac13} + 3\root 3\of 2 = 3\root 3\of 2 \end{displaymath}$

而且

$\begin{displaymath} \int_4^6 \frac1{\root 3 \of {(x-4)^2}}\,dx =\lim_{u\to4^+}\B... ...3\root 3\of 2 - \lim_{u\to4^+} 3(u-4)^{\frac13} =3\root 3\of 2 \end{displaymath}$

所以，問題 (4) 是可積的，答案是

$\begin{displaymath} (4) = 6\root 3\of 2 \end{displaymath}$

習題

請問
請問
請問
請問
請問