趨向無窮大的函數極限
以前我們探討的都是以下類型
的函數極限問題,其中 c 是一個實數。
對於這種問題,我們並沒有敘述嚴格的數學定義,
只是介紹了幾個重要的計算方法,趁這個機會簡單複習一下。
- 如果 f(x) 在 c 點連續,則上述極限就收斂到 f(c)
- 極限可能收斂、發散或不存在。
- 如果 f(x) 是個分式,而且分子收斂到一個非零實數,
但是分母收斂到 0,則上述極限發散。
- 如果 f(x) 是個分式,而且分子與分母都收斂到 0 或者都發散,
則屬於不定型式,要應用泰勒展開或者羅必達法則來計算。
這一節中,我們要探討以下類型的函數極限:
我們仍然不敘述嚴格的數學定義。只針對基本類型函數,介紹結果。
然後介紹運算性質。讀者目前只要會操作就好了。
基本類型函數
- 冪函數
-
冪數為 0
也就是常數極限的意思。令 c 是一個實數 (包括 0),則
冪數為整數
令 n 是一個正整數,則
而
例如
冪數為實數
令 r 是一個正實數 (包含有理數),為了方便起見 (而且不失其實用性),
我們只考慮 x > 0 的情況。則
例如
- 指數函數
-
如果考慮
基本運算規則
其實,所有規則都和
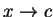 的極限計算規則相同,我們複習於此。
的極限計算規則相同,我們複習於此。
- 線性
若
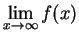 和
和
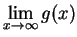 都收斂,而 c 是一個實數,則
都收斂,而 c 是一個實數,則
且
合稱為線性性質。
- 乘法律
若
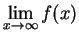 和
和
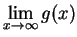 都收斂,則
都收斂,則
- 除法律
若
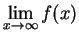 和
和
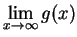 都收斂,而且
都收斂,而且
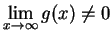 則
則
- 合成律
這其實是連續函數的定義。若
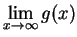 收斂到實數 T,而且 f(x) 在 x=T 處連續,則
收斂到實數 T,而且 f(x) 在 x=T 處連續,則
例如
- 夾擊定理
若
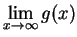 和
和
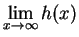 都收斂,而且存在一個數 A 使得
都收斂,而且存在一個數 A 使得
恆成立,則
例如考慮
因為對任何實數 x > 0 以下順序皆成立
而且
所以
- 不定型式
如果 f(x) 和 g(x) 都在
時發散。則
屬於
的不定型式。我們要提醒讀者,除了使用羅必達法則以外,
可能簡單地約分也就可以解決問題。例如
其他的不定型式還有
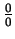 、
、
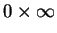 、
、
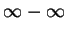 、
、
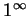 其處理方式都和
其處理方式都和
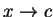 類型的不定型式相同,就不在贅述了。
類型的不定型式相同,就不在贅述了。
- 變數變換
那種
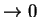 和
和
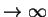 的極限問題經常可以互換。例如
的極限問題經常可以互換。例如
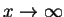 可以被代換成
可以被代換成
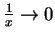 ,
反之亦然。舉例來說,以下兩者
,
反之亦然。舉例來說,以下兩者
和以下兩者
是相同的兩對問題。
習題
- 請問
- 請問
- 如果 f(x) 是一個「有界」函數;也就是說存在一個正數 M 使得
請證明
- 請問
- 請問
- 請問
- 請問
- 請問
- 請證明,對任意的正整數 n 都是
- 請問
- 請證明,對任意的正整數 n 都是
Created: Aug 5, 2001![]() 的極限計算規則相同,我們複習於此。
的極限計算規則相同,我們複習於此。
![]() 和
和
![]() 都收斂,而 c 是一個實數,則
都收斂,而 c 是一個實數,則
![]() 和
和
![]() 都收斂,則
都收斂,則
![]() 和
和
![]() 都收斂,而且
都收斂,而且
![]() 則
則
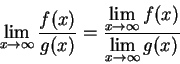
![]() 收斂到實數 T,而且 f(x) 在 x=T 處連續,則
收斂到實數 T,而且 f(x) 在 x=T 處連續,則
![]() 和
和
![]() 都收斂,而且存在一個數 A 使得
都收斂,而且存在一個數 A 使得
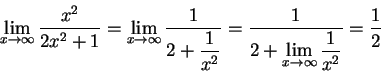
![]() 、
、
![]() 、
、
![]() 、
、
![]() 其處理方式都和
其處理方式都和
![]() 類型的不定型式相同,就不在贅述了。
類型的不定型式相同,就不在贅述了。
![]() 和
和
![]() 的極限問題經常可以互換。例如
的極限問題經常可以互換。例如
![]() 可以被代換成
可以被代換成
![]() ,
反之亦然。舉例來說,以下兩者
,
反之亦然。舉例來說,以下兩者