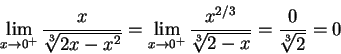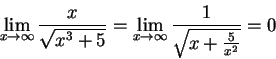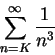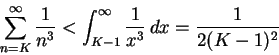冪函數的廣義積分
所有 (a,b] 或 [a,b) 區間中的「無限大函數」廣義積分,
經過函數的平移和鏡射之後,總是可以變成 (0,1] 區間內的問題。
例如,如果 f(x) 在 (a,b] 內連續,則 g(x) = f(x+a) 就變成在 (0,b-a] 中連續,而
就變成在 (0,1] 區間中連續。然後 f(x) 在 (a,b] 區間內的積分,
就變成 g(x) 在 (0,1] 區間內的積分
(這其實就是積分之變數變換技巧;f(x) 在 (a,b] 內的積值和
g(x) 在 (0,1] 內的積值,只差一個常數倍數。可見它們的廣義積分,
要是收斂就兩者都收斂,要是發散則兩者都發散。)
所有
因此,要概括性地討論廣義積分是否收斂的問題,
可以只討論在 (0,1] 內連續而且當
時會發散的函數;還有在
內連續的函數。
而所有這兩類型的函數,又可以簡化到冪函數 xp 來討論。
如果冪數 p > 0 則 xp 在 (0,1] 內根本是一個可拓展的連續函數,
所以它根本不是廣義積分,只是個普通的積分,而且在 [0,1] 內必定可積。
而如果冪數 p > 0 則 xp 在
內積分必定發散,這是因為
所以
當一個數會大到
那麼應該毫無疑問地,它自己也就發散到無窮大。
所以,對於正的冪數 p,根本沒有值得討論的廣義積分。
那麼,現在我們考慮負的冪數。也就是考慮
的兩種廣義積分。
首先,如果
則
因為
所以上述廣義積分當 p > 1 時發散。
當 p = 1 的時候,1/x 的反導函數是 ln(x),讀者可以自行檢驗,
其 (0,1] 內的廣義積分也發散。
所以,我們獲得結論:
再者,如果
則
因為
所以上述廣義積分當 p < 1 時發散。
當 p = 1 的時候,1/x 的反導函數是 ln(x),讀者可以自行檢驗,
其
內的廣義積分也發散。
所以,我們獲得結論:
以上 (1) 式和 (2) 式都很容易推導,所以請讀者不要背誦。
讀者或許會覺得 (1) 式和 (2) 式「互相相反」,其實沒有。
其實,它們倆透露了一個規則:
是一條界線:比它『大』的函數,廣義積分均發散;
比它『小』的函數,廣義積分均收斂。
上面那句話非常粗糙,但是應該可以提供讀者一個簡便的估計準則。
以上所謂的「大」和「小」,不是指係數而言,例如
雖然比
小,但是只是係數的差別,在冪數上,它們還是同一等級。
因此在 (0,1] 中的廣義積分仍然發散。
同理,
也不算是比
「大」。以上所說得「大」和「小」,指的是冪數,
也就是 (1) 和 (2) 式中的 p 。而為什麼會這樣說呢,
看以下兩張圖示就明白了。
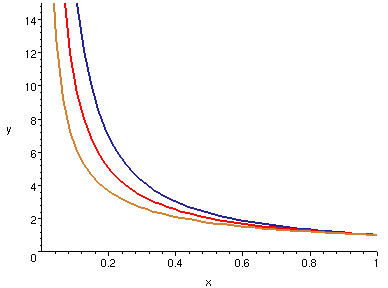
| x=0..1, p=0.8, p=1, p=1.2
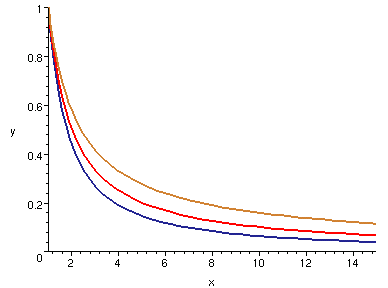
| x=1..15, p=0.8, p=1, p=1.2
|
|---|
| 
|
我們看到,紅色曲線是「界線」,而對照 (1) 式和 (2) 式,會收斂的曲線總在「下方」。
如果我們瞭解冪函數在 (0,1] 和
區間內的「函數大小」與「冪數大小」關係,就不會覺得 (1) 式和 (2) 式「相反」了,
它們不但沒有「相反」,反而是一個一致的現象。
為了避免一些細節引起的麻煩,我們從此只探討非負函數,也就是
f(x) >= 0 的函數。
如果遇到需要處理負值函數函數的時候,通常取其絕對值即可。
因此不再贅述。
在技術上,當我們面對一個 (a,b] 區間上的「無限大函數」廣義積分,
要怎樣才能斷定當
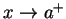 的時候,
的時候,
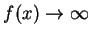 的速度比
的速度比
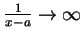 更慢 (因此曲線落在它的下方) 呢?試想,如果當 x 靠近 a 的時候,
存在某數 p < 1 使得
更慢 (因此曲線落在它的下方) 呢?試想,如果當 x 靠近 a 的時候,
存在某數 p < 1 使得
則因為
所以我們不難推論:如果
則
是可積的;否則不可積。
另方面,當我們面對一個「無限長區間」廣義積分,
要怎樣才能斷定當
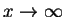 的時候,
的時候,
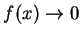 的速度比
的速度比
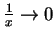 更快 (因此曲線落在它的下方) 呢?
試想,如果當 x 很大的時候,存在某數 p > 1 使得
更快 (因此曲線落在它的下方) 呢?
試想,如果當 x 很大的時候,存在某數 p > 1 使得
則因為
所以我們不難推論:如果
則
是可積的;否則不可積。
例如,考慮
這是一個 (0,1] 區間中的「無限大函數」廣義積分。因為
所以我們斷定 (3) 是可積的。
再考慮以下在無限長區間中的廣義積分:
因為
所以我們斷定 (4) 是可積的。
斷定一個廣義積分可積,並不代表知道它的答案。
例如前面的 (3) 式和 (4) 式,都確定是可積的,
可是我們卻無法以目前所學的積分技巧來算出答案。
那麼,這種判斷理論有什麼用呢?
它的用途是,因為數值方法寫成電腦程式之後,總是會算出一個答案,
如果不先斷定可積,則我們不能採信那個答案。
而判定了可積之後,就有許多可能的數值方法可資利用,
用來估計廣義積分的值。
至於那些數值方法,則不是一般微積分課程的討論範圍。
利用無限長廣義積分的下黎曼和,我們可以判斷某些無窮級數的收斂性,
還可以為它的極限求得一個上界。例如考慮
我們留給讀者自己去驗證,上述無窮級數是以下廣義積分問題
以 K, K+1, K+2, K+3, ... 為節點所做出的下黎曼和。因此,
所以我們不但斷定此無窮級數收斂,還知道了它的極限最大也不至於超過
1/(2*(K-1)^2)。
習題
- 請問
- 請問
是否可積?簡述理由。
- 如果
請問
簡述理由。
- 請問
是否可積?簡述理由。
- 如果
請寫出 C 和 g(x)。
- 請問
是否可積?簡述理由。
- 請問
是否可積?簡述理由。
- 請問
是否可積?簡述理由。
- 請問
是否可積?簡述理由。
- 請問
是否可積?簡述理由。
- 請問
是哪一個區間中的「無限大函數」廣義積分?是否可積?簡述理由。
- 請問,哪些數 p 可以使得以下廣義積分可積?簡述理由。[HH]
- 請問,哪些數 p 可以使得以下廣義積分可積?簡述理由。[HH]
Created: Aug 30, 2001

![]() 的時候,
的時候,
![]() 的速度比
的速度比
![]() 更慢 (因此曲線落在它的下方) 呢?試想,如果當 x 靠近 a 的時候,
存在某數 p < 1 使得
更慢 (因此曲線落在它的下方) 呢?試想,如果當 x 靠近 a 的時候,
存在某數 p < 1 使得
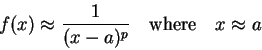
![]() 的時候,
的時候,
![]() 的速度比
的速度比
![]() 更快 (因此曲線落在它的下方) 呢?
試想,如果當 x 很大的時候,存在某數 p > 1 使得
更快 (因此曲線落在它的下方) 呢?
試想,如果當 x 很大的時候,存在某數 p > 1 使得